Security of Public-Key Cryptosystems
Published:
해당 포스트는 서울대학교 천정희 교수님의 암호론 강의를 기반으로 작성하였다. 이번 포스트에서는 ‘공개키암호의 안전성’에 대한 내용을 요약•정리하고자 한다.
1. 공개키암호의 안전성 개념 (Security of Public-Key Cryptosystems)
1) 공개키암호의 안전성 개념
- Targets
- One-wayness (OW): 역연산이 어려움 (hard to invert)
$\rightarrow$ 평문($e$)에서 암호문($c$)으로 갈 수 있지만 반대로는 불가하다!
(그렇지만 평문이 짝수인지 홀수인지 알 수 있다는 것을 알게 됨ㅠ) - Semantically Secure (Indistinguishable: IND): 부분 정보 노출 없음 (no partial information)
- 암호문 $c = E(m)$을 통해, 공격자가 평문 $m$에 대한 어떤 부분 정보도 추론할 수 없어야 한다.
- 즉, 암호문이 평문의 성질(예: 짝수/홀수, 길이, 특정 비트 값 등)을 드러내면 안 된다.
- 이를 만족할 때, 암호문은 평문에 대한 정보를 전혀 새지 않고 무작위처럼 보인다고 말한다. - Non-malleability (NM): 암호문으로부터 의미 있는 변형을 만들기 어려움
- $R$: 어떤 non-trivial relation (비자명한 관계)
- $E(M)$: 평문 $M$의 암호문
- NM조건: 공격자가 $E(M)$을 보고도 $E(R(M))$을 얻는 게 어렵다.
$\rightarrow$ 암호문을 변형해서 원래 평문과 관련된 다른 유효한 평문의 암호문을 얻을 수 없어야 한다.
$\Rightarrow$ Semantically Secure하지 않으면, Indistinguishable하지 않다!
- One-wayness (OW): 역연산이 어려움 (hard to invert)
📘 Indistinguishable 고차원 개념
- 정의
암호체계가 indistinguishable 하다는 것은 공격자가 두 개의 평문 $m_0, m_1$ 중에서
임의로 하나를 선택 후, 암호문 $E(m_b)$을 만들어서 $(m_0, m_1, E(m_b))$ 으로부터
$b$ 의 정보를 얻는 것이 어려워야 한다는 것을 의미한다.
- Attacks
- Passive attacks (Chosen Plaintext Attack: CPA)
- Active attacks (Chosen Ciphertext Attack: CCA)
2) Semantic Security (Indistinguisability: IND)
- 단계
- 공격자가 두 평문 $m_0, m_1$ 을 선택한다.
- 공격자는 무작위 비트 $b \in {0,1}$ 을 선택해서, 암호문 $c=E(m_b)$을 얻는다.
- 공격자는 $(m_0, m_1, c)$ 를 바탕으로 $b$를 추측한다.
- 공격자의 추측 $b’$ 가 실제 $b$와 같을 확률은 무작위 추측 수준($\frac{1}{2}$)을 유의미하게 넘지 않아야 한다.
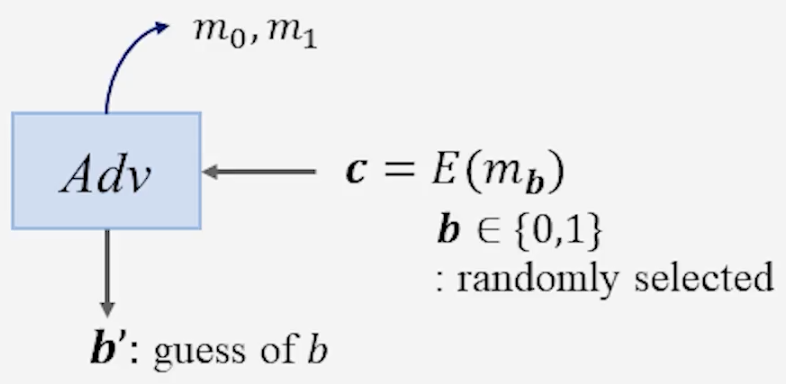
\(\therefore \Pr[b = b'] \leq \tfrac{1}{2} + \text{negl}(n)\) (여기서 $\text{negl}(n)$은 보안 매개변수 $n$에 대해 무시 가능한 값이다.)
3) Chosen Ciphertext Attack (CCA)
- CCA1 (Lunch time attack, Naor-Yung, ‘90)
- 공격자가 능동적 공격을 끝낸 후 암호문 $C_0$을 얻을 수 있는 상황
- CCA2 (Rackoff - Simon, ‘91)
- 공격자가 능동적 공격을 시작하기 전에 암호문 $C_0$을 얻을 수 있는 상황
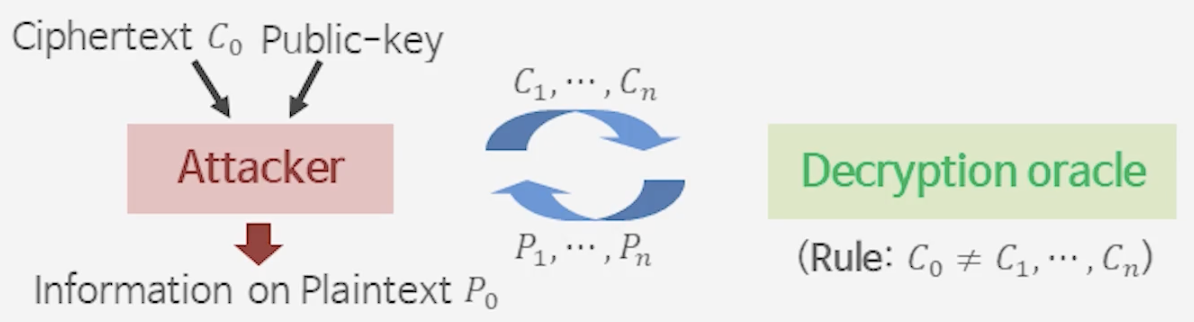
4) 공개키암호의 안전성 발전 역사
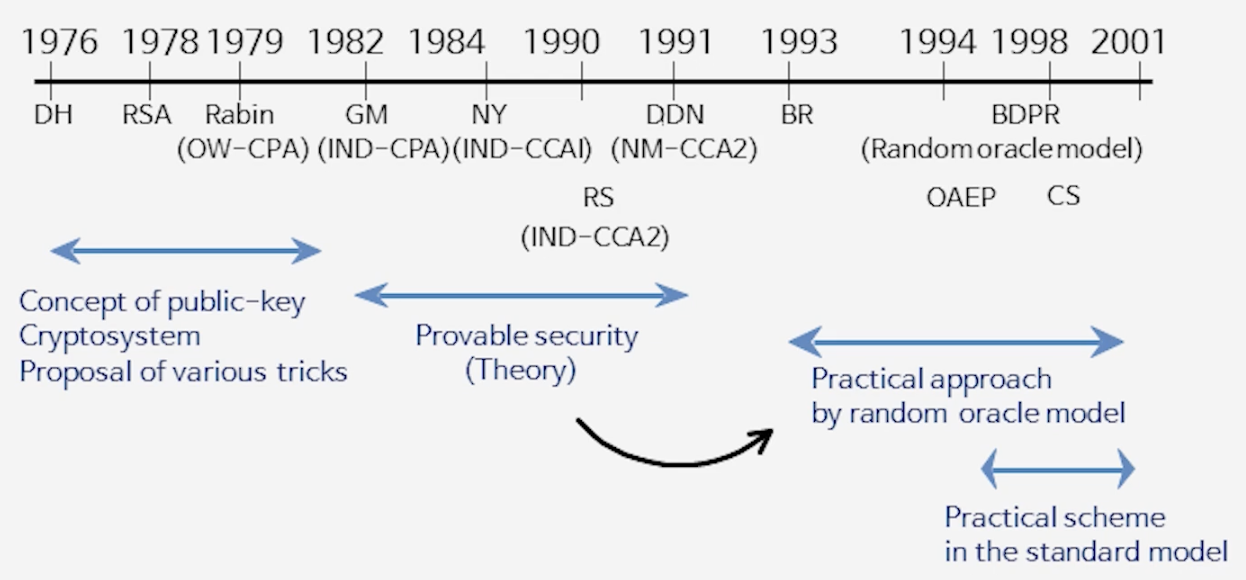
5) 가장 강력한 보안 (IND-CCA2) 암호체계 구성 방법
- Zero-Knowledge Proof 기반
- Dolev–Dwork–Naor (1991)
$\Rightarrow$ 비효율적 (Inefficient)
- 랜덤 오라클 모델 기반 (truly random function 가정)
- Bellare–Rogaway: OAEP (1994), PKCS#1–Ver.2 (1998)
- 대담한 가정: 해시 함수가 랜덤 함수와 구별 불가하다면 → 안전성 증명 가능!
- 물론 이 가정은 거짓. 해시 함수는 랜덤 함수처럼 작동하지만 실제로는 다르다.
📘 그럼에도 의미가 있었던 이유
- 그런 가정 위에서 RSA의 안전성을 처음으로 증명할 수 있었음
- 잘못된 가정을 출발점으로 했지만, 이후 점차 약한 가정을 사용하며 진짜 증명에 도달
- “틀린 가정이라도 증명 기법 발전의 촉매제 역할”을 했다는 점에서 큰 의의
- Fujisaki–Okamoto (1999), Pointcheval (2000)
- Okamoto–Pointcheval: REACT (2001)
$\Rightarrow$ 실용적 (Practical): 실제로는 무작위 함수 대신 일방향 함수(one-way functions)를 사용
- Bellare–Rogaway: OAEP (1994), PKCS#1–Ver.2 (1998)
- 랜덤 함수 없이도 가능한 실용적 구성
- 이산로그에 기반한 Cramer–Shoup (1998)
→ 표준 모델에서 처음으로 IND-CCA2 안전성을 만족하는 실용적 공개키 암호체계
- 이산로그에 기반한 Cramer–Shoup (1998)
6) Naïve RSA와 ElGamal의 안전성
- RSA는 malleable (변형 가능)하다.
📘 malleable 의미
RSA에서 $c = m^e \pmod{n}$ 일 때, \(2^{e} \cdot c \equiv (2m)^e \pmod{n}\)
→ 공격자는 원래 메시지 $m$을 몰라도, $2m$에 해당하는 새로운 암호문을 쉽게 만들 수 있다.
→ 즉, 암호문에서 평문과 연관 있는 다른 암호문을 생성할 수 있으므로 Non-malleability(NM)를 만족하지 못한다. - ElGamal (유한체 위에서 정의된 경우)
→ IND 보안(Indistinguishability)을 만족하지 않는다.📘 왜 IND가 깨지는가?
ElGamal 암호문은 $(g^r, m \cdot h^r)$ 꼴이다.
- 여기서 $g$는 생성원(generator), $r$은 랜덤 값.
- 하지만 공격자는 두 번째 성분을 통해 메시지가 $g$의 짝수 지수 꼴인지, 홀수 지수 꼴인지 판정할 수 있다.
→ 따라서 평문에 대한 일부 정보가 노출되어, 구별 불가능성(IND)이 깨진다.
- EC-ElGamal (타원곡선 기반)
→ IND-CCA2 보안을 만족하지 않는다.
📘 추가 설명: Generic Group vs Elliptic Curve Group
Generic Group Model (제네릭 군 모델)
공격자가 군의 원소를 다루지 못하고, 단지 "블랙박스 연산(곱셈·역원·동등성 검사)"만 가능하다고 가정
→ 이 모델에서는 ElGamal이 IND-CPA 보안을 만족한다.Elliptic Curve Group (타원곡선 군, 실제 구현)
실제 타원곡선 구조에서는 공격자가 곡선의 수학적 성질을 활용할 수 있음
즉, 공격자가 구체적인 타원곡선 구조를 활용한 공격도 가능해짐
→ 따라서 EC-ElGamal은 강한 보안(특히 IND-CCA2)을 만족하지 못한다.
7) Secure Conversion: 실용적이고 안전한 암호 만들기
Primitive 암호체계 (예: RSA, ElGamal)
→ 그대로 버리는 것이 아니라, 이를 기반으로 변환(conversion)을 적용할 수 있다.- 아이디어:
- primitive가 특정 조건 (예: trapdoor one-way, IND-CPA)을 만족하면
- 변환 상자(conversion)에 넣어 자동으로 IND-CCA2 안전한 암호체계를 얻을 수 있음
→ 이를 secure conversion이라 부른다.
- 연구적 의미:
- primitive의 안전성 증명 (예: trapdoor one-way, IND-CPA)는 비교적 쉽다.
- 하지만 IND-CCA 보안 증명/설계는 어렵다.
- 따라서 연구자들은 “IND-CPA 스킴 → conversion 적용 → IND-CCA2 스킴” 방식으로 접근했다.
📘 IND-CPA (Chosen Plaintext Attack 보안)
- 공격자가 원하는 평문 $m_0, m_1$을 선택한다.
- 암호문은 무작위로 선택된 $m_b$의 암호문 $c = E(m_b)$로 주어진다.
- 공격자의 목표: $b \in {0,1}$을 맞추는 것.
IND-CPA 보안 조건:
\(\Pr[b = b'] \leq \tfrac{1}{2} + \text{negl}(n)\) → 무작위 추측과 유의미하게 구별되지 않아야 한다.→ 암호문만 보고도 평문을 알아내기 어려워야 한다.
📘 IND-CCA2 (Chosen Ciphertext Attack 보안)
- 공격자는 복호화 오라클을 이용해 임의의 암호문 $c_1, \dots, c_n$을 복호화해볼 수 있다.
- 단, 목표 암호문 $c^*$ 자체는 복호화할 수 없다.
- 목표: $c^* = E(m_b)$에 대해 $b \in {0,1}$을 맞추는 것.
IND-CCA2 보안 조건:
\(\Pr[b = b'] \leq \tfrac{1}{2} + \text{negl}(n)\) → 복호화 오라클을 쓸 수 있어도 무작위 추측 수준 이상 맞출 수 없어야 한다.→ 암호문만 보는 게 아니라, 다른 암호문을 복호화해보는 강력한 능력을 줘도 여전히 평문을 알아내기 어려워야 한다.
2. ElGamal의 IND-CPA 안전성 (IND-CPA Security of ElGamal)
1) ElGamal의 IND-CPA 안전성 정의
- $G$: 소수 차수 $p$를 갖는 (순환) 가환군, 생성원 $g \in G$
- DDH 문제 (Decision Diffie–Hellman)
$\colon$ 주어진 $(g, g^x, g^y, g^z)$에 대해 $z \stackrel{?}{=} xy \pmod p$를 판정
📘 ElGamal과 DDH의 관계
**“ElGamal이 깨지면 DDH도 깨진다 → 따라서 DDH가 안전하면 ElGamal도 안전하다”
- Interactive Assumption (상호작용 가정)
- ElGamal의 안전성을 정의하려면 공격자(Adversary)와 도전자(Challenger)가
메시지를 주고받는 시나리오를 설정해야 한다. - 수학적으로 깔끔하게 표현하기 어려워, 공격자가 존재하지 않는다는 식으로만 보안을 표현할 수 있다.
- ElGamal의 안전성을 정의하려면 공격자(Adversary)와 도전자(Challenger)가
- Non-Interactive Assumption (비상호작용 가정)
- 반면 DDH 문제는 단순하다.
- 주어진 $(g, g^x, g^y, g^z)$가 Diffie–Hellman를 만족하는 지 판별하기만 하면 된다.
- 공격자와의 상호작용이 필요 없고, 문제 자체를 풀 수 있느냐 없느냐만 보면 된다.
2) ElGamal의 IND-CPA 보안 실험
- 도전자 $C$가 비밀키 $k \xleftarrow{$} \mathbb{Z}_p$를 뽑고 공개키 $g^k$를 만든다.
- 도전자 $C$는 공개키 $g^k$를 공격자 $A$에게 보낸다.
- 공격자 $A$는 두 평문 $m_0, m_1$을 선택해 도전자 $C$에게 보낸다.
- 도전자 $C$는 무작위 $r \xleftarrow{$} \mathbb{Z}_p$와 무작위 비트 $b\in{0,1}$를 뽑고
암호문 $c=(g^r,\; m_b \cdot (g^k)^r)$를 $A$에게 전달한다. - 공격자 $A$는 $b$를 추측해 $b’$를 제시한다.
(보안 조건: $\Pr[b’=b] \le \tfrac12 + \mathrm{negl}(n)$)
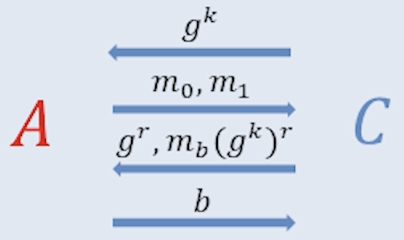
3) ElGamal의 IND-CPA 보안 실험 증명
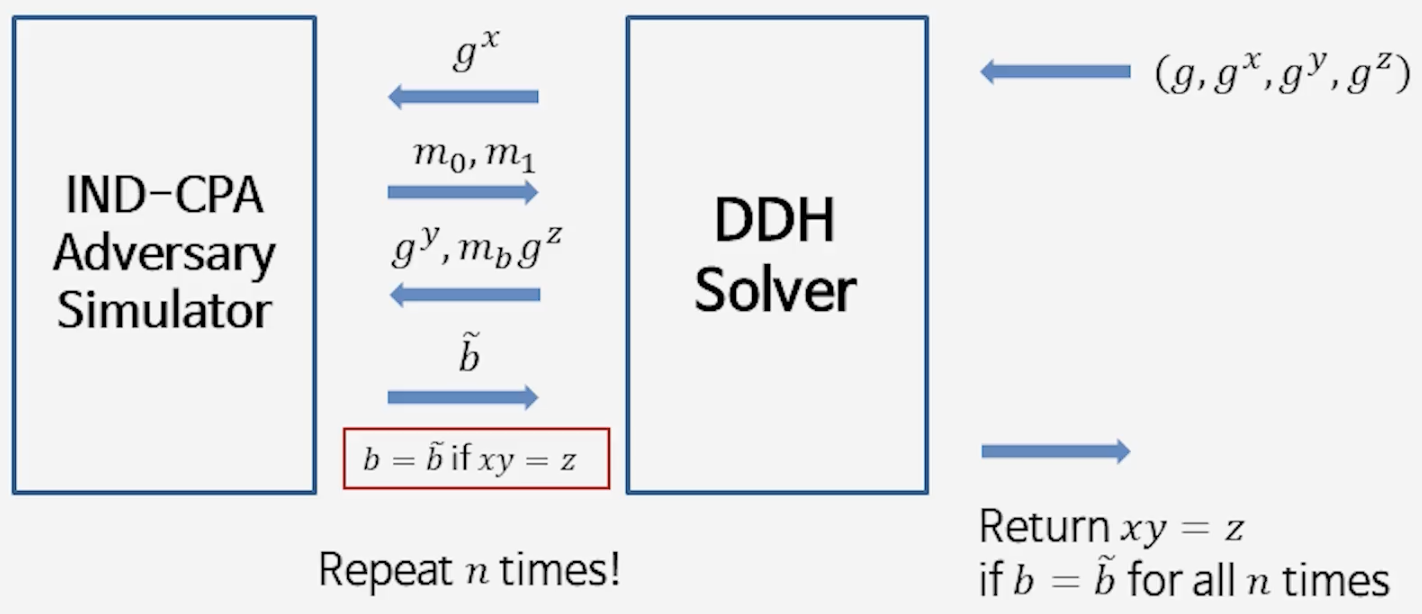
- 가정
- 공격자가 아주 가끔이라도 $b$를 잘 맞출 수 있다고 하자.
- (이득이 작아도 반복/증폭 기법으로 항상 잘 맞추는 공격자로 바꿀 수 있음.)
- DDH 문제와 연결
- 우리가 받은 문제: $(g, g^x, g^y, g^z)$
- 목표: $z = xy$인지 아니면 랜덤인지 판별
- 공격자 활용
- $g^x$ → 공개키처럼 전달
- $g^y$ → 난수 $r$ 대신 사용
- $g^z$ → 암호문의 두 번째 성분 자리에 넣음
- 판정 원리
- 만약 $z=xy$: 공격자가 받은 건 올바른 암호문
→ $b$를 잘 맞춤 → DDH = “예 (Yes)” - 만약 $z\neq xy$: 공격자가 받은 건 잘못된 암호문
→ 공격자는 랜덤처럼 동작 → $b$를 못 맞춤 → DDH = “아니오 (No)”
- 만약 $z=xy$: 공격자가 받은 건 올바른 암호문
- 반복 실험과 분포 판정
- 실제 증명에서는 단 한 번의 실행만으로 끝내지 않는다.
- 공격자가 무작위 추측(50%)보다 유의미하게 높은 확률로 $b$를 맞추는지,
여러 번 반복 실험을 통해 분포를 기준으로 판정한다.
📘 비유: 공격자를 시장에서 사온다?
- 가정
- ElGamal을 무너뜨릴 수 있는 공격자가 어딘가에 존재한다고 치자.
- 이 공격자는 아무 입력에나 작동하지 않고, CPA 실험 절차에서만 동작한다.
- 시장 비유
- 마치 “공격자를 파는 시장”에서 그런 컴퓨터를 하나 사왔다고 생각한다.
- 그 공격자는 우리가 준 공개키·평문·암호문 시나리오 안에서만 움직인다.
- 실제로 있는 건 아니지만, 사고실험(thought experiment)으로 가정한다.
- Reduction (귀속 아이디어)
- 우리가 진짜로 풀고 싶은 건 DDH 문제: $(g, g^x, g^y, g^z)$ 네 값이 주어졌을 때,
마지막 값 $g^z$가 정말 $g^{xy}$인지, 아니면 랜덤 값인지 구별할 수 있는지를 묻는 문제다. - 그런데 ElGamal 공격자를 블랙박스처럼 활용하면, 이 판별을 할 수 있다.
- 즉, ElGamal 공격자가 $b$를 잘 맞출 수 있다면 → $z=xy$인지 여부도 알아낼 수 있다.
- 우리가 진짜로 풀고 싶은 건 DDH 문제: $(g, g^x, g^y, g^z)$ 네 값이 주어졌을 때,
- 작은 이득도 괜찮다
- 공격자가 $b$를 무조건 잘 맞추지 않아도 된다.
- 무작위 추측보다 아주 조금이라도 잘 맞춘다면,
반복 실행과 증폭 기법으로 충분히 유의미한 공격자로 바꿀 수 있다.
✅ 핵심
- ElGamal 공격자가 있다면 → DDH 해결기가 만들어진다.
- DDH가 어렵다면 → ElGamal 공격자는 없다.
- 따라서 DDH가 안전하면 ElGamal도 IND-CPA로 안전하다.
3. RSA암호의 IND-CCA2 안전성 (IND-CCA2 Security of RSA)
1) RSA의 IND-CCA2 안전성 설명
- IND-CPA와의 차이점
- CPA에서는 공격자가 공개키와 암호문만 보고 $b$를 맞추는 실험을 한다.
- CCA2에서는 공격자가 복호화 오라클(Decryption Oracle)에 질문할 수 있다.
- 즉, 원하는 암호문을 입력하면 평문을 돌려받는 환경을 가정한다.
- 👉 오라클(Oracle)이란?
마치 신탁처럼, 우리가 질문(입력)을 던지면 그에 맞는 답(출력)을 돌려주는 가상의 상자를 말한다. 실제로 존재하지는 않지만, 보안 모델을 정의하기 위해 가정한다.
- 문제점
- DDH Solver는 비밀키 $x$를 모르기 때문에 직접 복호화를 해줄 수 없다.
- 하지만 공격자는 “복호화를 요청할 수 있다”는 조건 하에서만 동작한다.
- 따라서 Solver가 공격자에게 진짜 복호화를 해주는 척(시뮬레이션) 해야 한다.
- 결과
- 공격자는 실제로는 복호화한 결과물을 받지 못하지만, 마치 받는 것처럼 “착각”하게 된다.
- 이렇게 시뮬레이션을 만들어야만 CCA2 환경에서의 안전성을 증명할 수 있다.
- 따라서 IND-CCA2 보안 증명은 CPA보다 훨씬 어렵다.
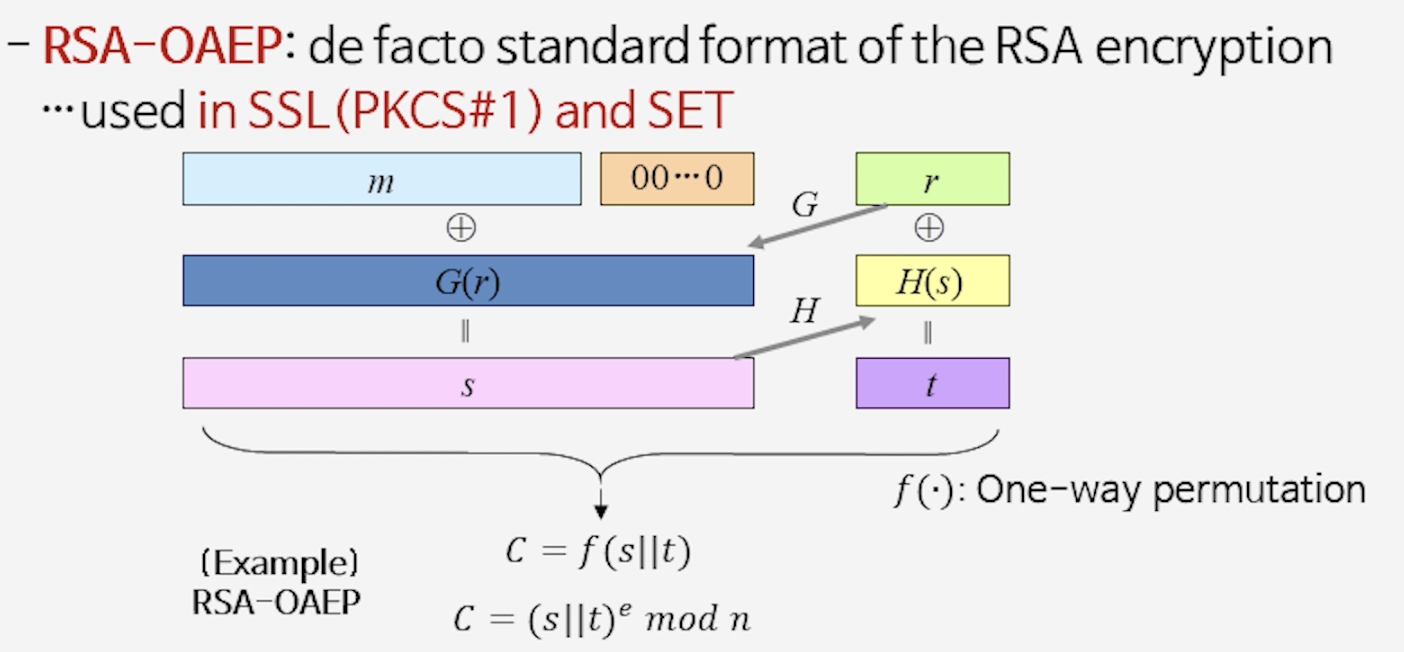
2) OAEP (Optimal Asymmetric Encryption Padding)
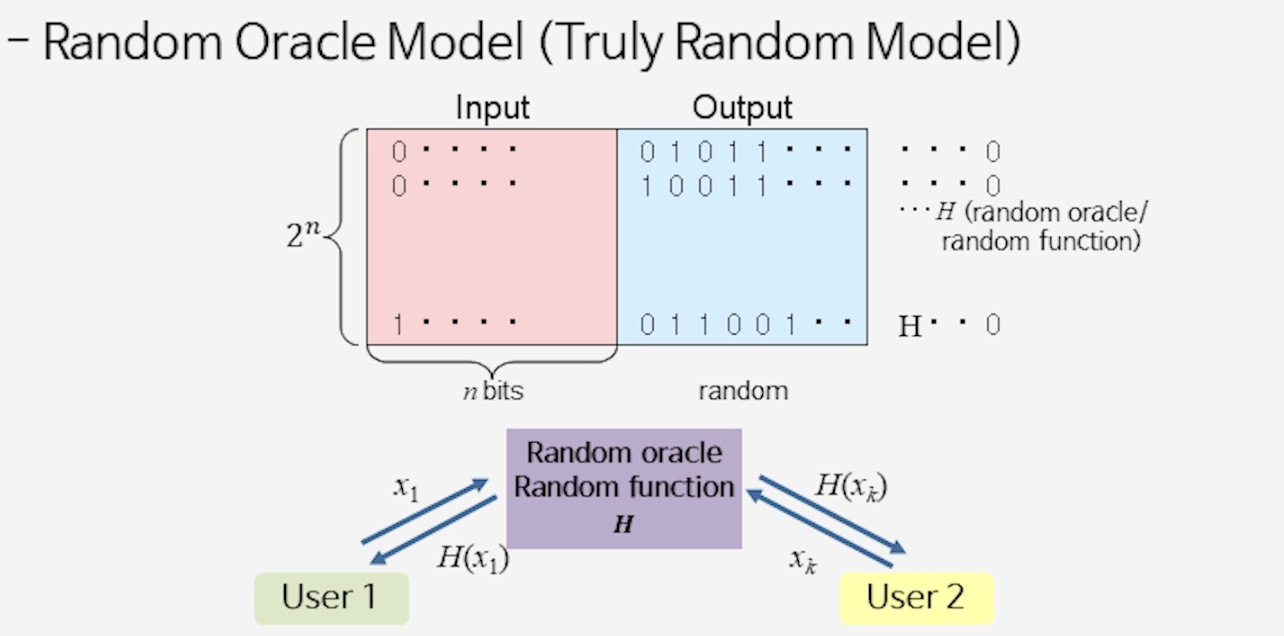
📘 랜덤 오라클(Random Oracle) 가정
- 해시 함수 $H$를 무작위 신탁(oracle)처럼 다룬다.
- 가정 조건
- 물어보기 전에는 $H(x)$ 값을 알 수 없다.
- 같은 입력 $x$를 넣으면 항상 같은 답 $H(x)$를 준다.
- 실제 해시는 계산 가능한 함수이므로 진짜 “랜덤 오라클”은 아니다.
- 하지만 증명을 위해 “랜덤 오라클처럼 동작한다”고 가정한다.
- 아이디어
- 평문 $m$에 무작위 값 $r$을 섞어 해시 함수 $G, H$를 적용하고,
결과를 다시 조합하여 $(s||t)$라는 블록을 만든 뒤 RSA로 암호화한다. - $f$: 일방향 함수 (예: $x \mapsto x^e \bmod n$)
- 결과 암호문: $C = f(s||t)$
- 평문 $m$에 무작위 값 $r$을 섞어 해시 함수 $G, H$를 적용하고,
- 특징
- $G, H$를 랜덤 오라클로 가정하여 증명을 진행한다.
- 이 padding 방식을 사용하면 RSA-OAEP라는 안전한 RSA 스킴이 된다.
- 실제로 PKCS#1 v2에 표준으로 채택되어 SSL, SET 등에서 사용되었다.
3) RSA-OAEP의 보안 증명 (랜덤 오라클 모델)
- 가정
- $f$는 일방향 함수 (예: RSA 지수승 모듈로 $n$).
- $H$는 해시 함수이지만, 증명에서는 랜덤 오라클로 취급한다.
- 증명 아이디어
- 만약 공격자가 RSA-OAEP를 구별할 수 있다면, 결국 $f$를 역산할 수 있다는 걸 보인다.
- 즉, 구별 가능성(distinguishability)이 곧 역산 가능성(invertibility)을 의미한다.
- 결론
- 랜덤 오라클 모델 하에서, RSA-OAEP는 IND-CCA2 안전성을 만족한다.
- 따라서 RSA에 padding을 잘 설계하면, 이론적으로도 안전성과 실용성을 모두 확보할 수 있다.