Post-Quantum Cryptography
Published: Updated:
해당 포스트는 서울대학교 천정희 교수님의 암호론 강의를 기반으로 작성하였다. 이번 포스트에서는 ‘양자내성암호’에 대한 내용을 요약•정리하고자 한다.
1. 양자내성(Quantum-resistant) 공개키암호
1) 양자 컴퓨터의 전망
- 약 15년 이내에 기존 암호를 공격할 수준의 양자 컴퓨터 도래 예상
📘 양자컴퓨터, 정말 만들 수 있을까?
양자컴퓨터, 아직은 Open Problem
- 양자컴퓨터를 충분히 큰 규모로 만들 수 있느냐는 아직도 open problem이다.
- 현재 우리는 소규모의 양자 비트(Qubit)를 다루는 장치는 만들었지만, 이를 scalable하게 확장할 수 있을지는 불확실하다.
- 양자컴퓨터는 0과 1을 동시에 다루지만, 이로 인해 잡음(noise)와 decoherence가 심각해지고, 여러 큐비트를 동시에 안정적으로 제어하는 것이 매우 어렵다.
- 그래서, 예를 들어 1,000큐비트로 확장하게 되면 오류(Error)가 너무 커진다.
양자컴퓨터의 두 가지 구현 방식
- Quantum Gate 방식: 전통적으로 암호학에 위협적인 방식이지만, 현재 발전 속도는 더딘 편이다.
- Quantum Annealing(어닐링) 방식: D-Wave, Google 등에서 이미 수백 큐비트까지 구현했으나, 이 방식은 암호를 다항식 시간 내에 깨지는 못한다.
대신, 검색·최적화 문제를 빠르게 푸는 데 유용하며, 실제로 산업 응용에서 활발히 연구 중이다. - 따라서, 암호를 직접적으로 해독할 수 있는 게이트 기반 양자컴퓨터가 언제 등장할지는 불확실하다.
어떤 전문가는 15년, 또 어떤 전문가는 150년을 예상할 정도로 의견 차이가 크다.
- 현재 널리 쓰이는 모든 공개키 암호(ECC/RSA 등)은 Shor’s Algorithm 때문에 공격 가능
📘 Shor's Algorithm 자세히 보기
- Shor의 알고리즘은 인수분해와 이산로그 문제의 복잡도를 지수적(exponential)에서 다항식(polynomial) 수준으로 낮춘다.
- 따라서 현재 우리가 사용하는 RSA, ECC 같은 공개키 암호는 양자컴퓨터에서 효율적으로 깨질 수 있다.
- 예: 약 1,000 큐비트 정도의 양자컴퓨터가 현실화되면 RSA-2048 수준의 암호도 짧은 시간 안에 풀릴 수 있다고 예측한다.
- 반면, 대칭키 암호/해쉬 함수는 키의 길이, 해쉬의 길이를 두 배로 늘리면 기존 수준의 보안성 유지 가능
2) Contemporary Cryptography
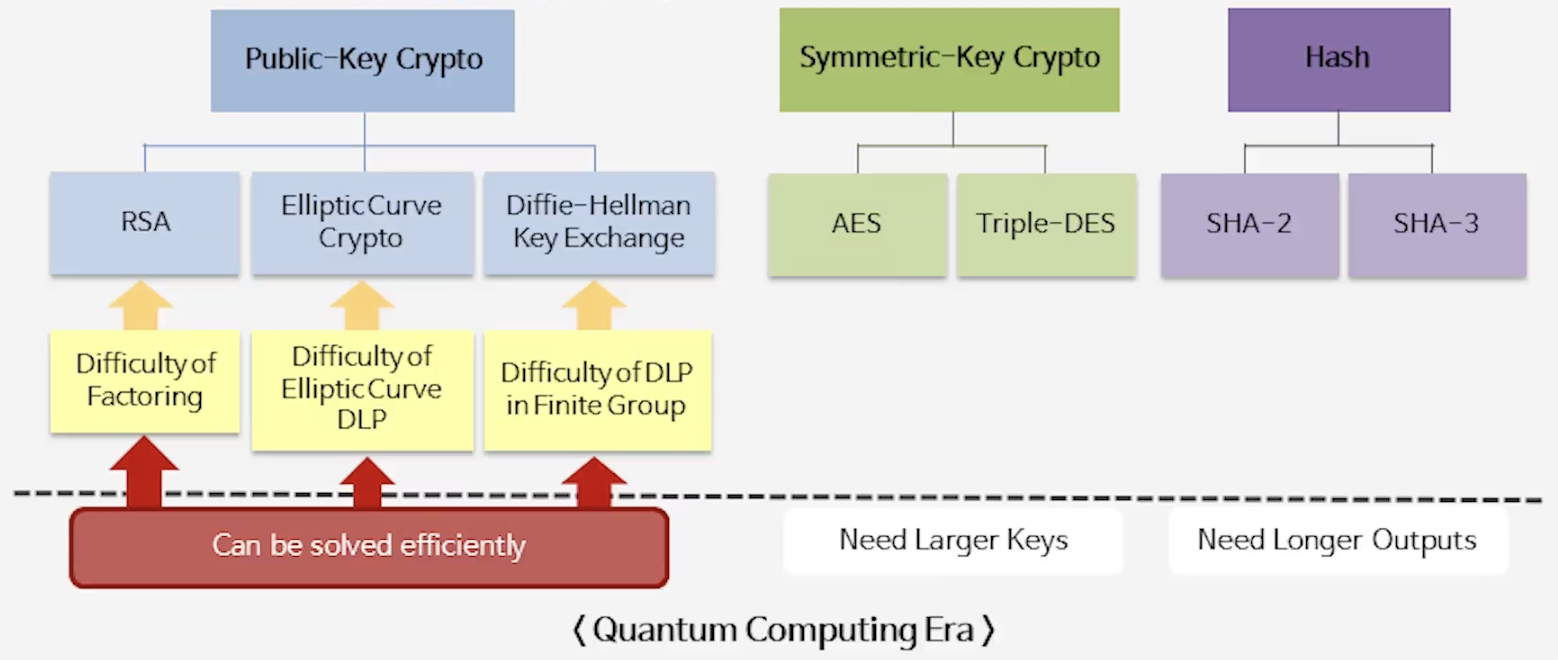
- 공개키 암호 (RSA, ECC, DH): Shor 알고리즘 때문에 안전하지 않음 → 비트 수 늘려도 소용 없음
- 대칭키 암호 (AES 등): 키 길이를 2배로 늘리면 안전성 유지 가능 (예: AES-256 권장)
해시 함수 (SHA 계열): 출력 길이를 3배로 늘려야 같은 수준의 보안성 유지 가능
- 요약: 누가 무엇에 영향주는가
- Shor’s algorithm: 공개키 암호(인수분해·이산로그 기반)를 양자환경에서 다항식 시간(polynomial time) 내에 풀어버리는 알고리즘 → 공개키 계열은 근본적 위협
- Grover’s algorithm: 대칭키/해시의 무차별 공격을 제곱근(quadratic) 속도로 가속화하는 알고리즘 → 완전 붕괴는 아니며, 키/출력 길이를 늘려 방어 가능
📘 왜 이렇게 되는 걸까?
- 공개키 (Shor)
- 고전적 최선: 인수분해·이산로그는 지수 시간(대략 $(2^{n})$ 또는 유사) 소모
- Shor: 이를 다항식 시간(예: poly($n$))으로 해결 → 비트 길이 확대만으로는 방어 불가
- 대칭키 (Grover)
- 고전적 무차별 검색: $O(2^{n})$ (키 길이: $n$)
- Grover: $O(2^{\frac{n}{2}})$으로 가속 — 즉 제곱근(Quadratic) 속도 향상
- 결과: 키 길이를 2배 하면 기존 수준의 보안 유지 가능 (예: AES-128 → AES-256 권장)
- 해시(충돌/프리이미지)
- 고전적 충돌 저항: $2^{\frac{n}{2}}$ (출력 길이: $n$)
- 양자 영향 하의 충돌/프리이미지 복잡도는 알고리즘과 공격 모델에 따라 달라지지만, 실무에서는 출력 길이를 충분히 늘림(권장: 약 3배 규칙)으로 안전성을 확보하는 관점이 사용
- 따라서 “128비트 수준의 안전성”을 목표로 하면 출력 길이를 256비트가 아니라 더 늘려(약 384비트 권장)야 한다는 주장으로 정리되는 경우가 있음
3) Post-Quantum Cryptography (1)
- 2016년, 미국 국가안보국(NSA)은 “머지않은 미래(not too distant future)에 Post-Quantum Cryptography (PQC)로 전환하겠다”고 발표
- 곧바로 미국 국립표준기술연구소(NIST)가 PQC 표준화 프로젝트를 시작하면서 오늘날의 Kyber, Dilithium 등 PQC 알고리즘 경쟁이 본격화
- 목표: Post-Quantum 공개키 암호(Encryption / Signature / Key Exchange)의 표준화
📘 당시 상황을 조금 더 살펴보기
- 당시 미국 정부는 Suite A/B 암호 체계를 따랐는데, Suite B에는 AES와 ECC를 포함한다
- 즉, 미국과 외국 정부가 안전하게 통신하려면 ECC 지원이 필수였다.
- 그런데 NSA가 ECC 도입을 중단하고 PQC로 전환하겠다고 선언하면서, 사실상 전 세계가 따라야 하는 신호가 되었다.
- NSA 발표 직후, NIST는 2016년 가을 Call for Proposals, 2017년 Submission 마감 일정을 공개하며 PQC 표준화 작업에 착수했다.
4) Post-Quantum Cryptography (2)
- 양자내성암호의 전제 조건
- 가설 1. $P ≠ NP$
→ 양자컴퓨터가 등장해도 $NP$ 문제 전체를 쉽게 풀 수 있다는 근거는 없다. - 가설 2. NP-hard 기반 안전성
→ 암호는 보통 NP-hard 문제와 동치가 아니라, 그 위에 기반한다고 본다.
📘 더 자세히 보기
- 가설 1 (P ≠ NP)
- 퀀텀 알고리즘은 병렬화와 유사한 성질을 보이지만, NP 문제 전체를 풀 수 있다는 증거는 없다.
- 따라서 P와 NP의 분리는 유지된다고 보는 것이 일반적이다.
- 가설 2 (기반 vs. 동치)
- 암호 설계에서 특정 NP-hard 문제와 정확히 동치임을 보장할 수는 없다.
- 하지만 “그 문제를 기반으로 한다(based on)” 정도면 연구자 사회에서 충분히 인정한다.
- 예: RSA는 인수분해와 동치는 아니지만, 인수분해 문제에 기반해 안전성을 설명한다.
- 가설 1. $P ≠ NP$

- Lattice-based가 주목받는 이유
- 보안성: 난이도가 높은 격자 문제(lattice problems) 에 기반 (NP-hard)
- 효율성: 구현이 빠르고, 실제 하드웨어/소프트웨어에 적합
- 범용성: 동형암호(HE), 신원기반암호(IBE) 등 다양한 응용 가능
- 동형암호(HE): 암호화된 상태에서 연산을 직접 수행할 수 있는 암호
- 신원기반암호(IBE): 이메일 주소 같은 신원 자체를 공개키로 삼는 암호
5) 경량 (Light Weight) 공개키암호
- 기존 공개키 암호의 기반 난제: 지수승 연산 (예. RSA, ECC → $a \mapsto a^b$)
- 지수 연산은 본질적으로 계산량이 크고, 효율성에도 한계가 있음
- 그렇다면, “지수승 대신 곱셈만으로도 안전한 암호를 만들 수 없을까?”란 질문이 나옴
- 곱셈은 지수승보다 계산이 훨씬 빠르지만 (제곱 정도의 계산량),
$a \mapsto ab$는 너무 단순해서 일방향 함수로 쓰기에는 안전성 부족
- 곱셈은 지수승보다 계산이 훨씬 빠르지만 (제곱 정도의 계산량),
📘 Lattice 접근법
- 격자 기반 암호는 단순 곱셈 $ab$에 노이즈(잡음)를 더해서 문제를 어렵게 만든다.
- $a \mapsto ab + \text{noise}$ 형태
- 계산량은 quadratic 수준을 유지하면서도, 노이즈 때문에 문제는 어렵게 정의된다.
- 노이즈가 들어가면 단일 해답이 아니라 많은 경우의 수(case)가 생겨서 공격이 어렵다.
→ 이런 성질 덕분에 Lattice 기반 암호는 효율성(빠름)과 안전성(어려움) 을 동시에 노릴 수 있다.
2. 격자기반 양자내성암호
1) Geometry of Numbers: Lattices (1)
- 격자란 무엇인가?
- 격자(Lattice)는 $\mathbb{R}^n$ 안에 있는 이산적인(discrete) 점들의 집합
- 이산적이란? 임의의 격자점에서 작은 원을 그리면, 그 안에는 자기 자신만 있고 다른 격자점은 들어오지 않는다.
- 일차독립 벡터 $v_1, \dots, v_m \in \mathbb{R}^n$이 주어지면, \(L = \mathbb{Z}v_1 + \cdots + \mathbb{Z}v_m\) (선형결합)로 정의
📘 기저 (Basis)와 기저 행렬
- 기저 (Basis)
- $v_1, \dots, v_m$을 격자의 기저(basis)라고 한다.
- 이 기저 벡터들을 정수배해서 나오는 모든 점들이 격자점이다.
- 벡터공간의 기저와 비슷하지만, 차이가 있다 → 벡터공간은 실수배/유리수배를 허용하지만, 격자는 정수배만 허용한다.
- 기저 행렬 (Basis Matrix)
- 기저 벡터들을 모아 $B = [v_1 ; v_2 ; \cdots ; v_m]$라고 하면,
모든 격자점 $v$는 \(v = Bx, \quad x \in \mathbb{Z}^m\) 형태로 쓸 수 있다.
- 기저 벡터들을 모아 $B = [v_1 ; v_2 ; \cdots ; v_m]$라고 하면,
📘 격자의 부피 (Determinant)
- 격자의 부피(Det(L))는 기저 벡터들이 만드는 평행다면체(parallelepiped)의 부피와 같다.
- \(\det(L) = \det[v_1 ; v_2 ; \cdots ; v_m]\) 로 정의된다.
- 💡 직관적으로, 2차원 (평행사변형의 넓이), 3차원 (평행육면체의 부피), 4차원 이상 (일반화된 평행다면체의 부피)
- 단, 정사각행렬이 아닐때는?
- 예: 3차원 공간에 벡터가 두 개만 있으면 3×2 행렬 → 정사각형 아님
- 이 경우, 두 벡터가 span하는 2차원 평면 위에서 생각한다.
- 즉, 그 평면 안에서 2×2 행렬로 다시 보고, 그 평행사변형의 넓이로 정의할 수 있다.
📘 정수론과 격자의 연결
- 정수론에는 원래 거리 개념이 없다.
→ 예: 모듈러 $p$에서 2와 5 중 어느 쪽이 더 크다고 말할 수 없다. - 하지만 격자를 도입하면 거리 개념을 가져올 수 있고, 덕분에 “가장 작은 해(솔루션)” 같은 문제를 논할 수 있다.
- 응용 예시: Four Square Theorem
→ 모든 자연수는 네 제곱수의 합으로 쓸 수 있다
\(n = a^2 + b^2 + c^2 + d^2\)
- 응용 예시: Four Square Theorem
- 격자(Lattice)는 $\mathbb{R}^n$ 안에 있는 이산적인(discrete) 점들의 집합
- 격자와 벡터공간의 차이
- 벡터공간에서는 실수( $\mathbb{R}$ )나 유리수( $\mathbb{Q}$ ) 배수가 허용
→ 예: 벡터를 $0.1$배, $1.5$배 등으로도 만들 수 있음 - 격자에서는 정수($\mathbb{Z}$) 배수만 허용
→ 예: 벡터를 $1$배, $2$배, $-3$배 하는 식
$\therefore$ 격자는 벡터공간의 “부분집합”이지만, 모든 점이 격자점인 것은 아니다.
- 벡터공간에서는 실수( $\mathbb{R}$ )나 유리수( $\mathbb{Q}$ ) 배수가 허용
- 격자의 어려운 문제들
- Shortest Vector Problem (SVP): 0이 아닌 가장 짧은 벡터를 찾는 문제 (어렵다).
- Closest Vector Problem (CVP): 임의의 점이 주어졌을 때 가장 가까운 격자점을 찾는 문제 (역시 어렵다).
- 이 난제들이 바로 격자 기반 암호의 안전성을 뒷받침한다.
2) Geometry of Numbers: Lattices (2)
- Shortest Vector Problem (SVP):
격자 $L$이 주어졌을 때, 0이 아닌 벡터 중에서 가장 짧은 벡터를 찾으시오.
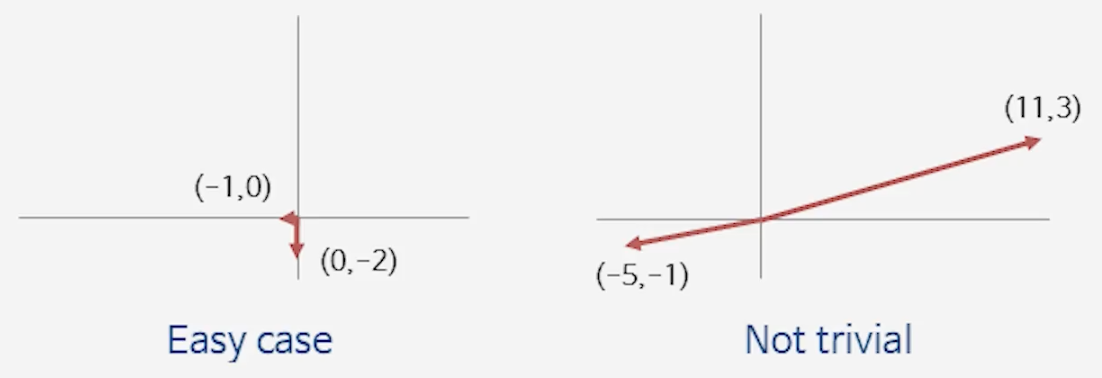
📘 어떤 경우에 어려울까?
- 직교 기저(orthogonal basis)일 때는 쉽다.
- 기저 벡터들이 서로 수직이라면, 임의의 점에서 정사영(projection)을 이용해 쉽게 가까운 격자점이나 최소 벡터를 찾을 수 있다.
- 예: (–1, 0)이나 (0, –2) 같은 경우 → 바로 확인 가능.
- 기저가 “누워 있는 경우(직교가 아닌 경우)”에는 어렵다.
- 기저 벡터들이 수직에서 멀어질수록, 한 점에 대해 가까운 후보 격자점이 여러 개 생긴다.
- 정사영 방식이 통하지 않아, 최소 벡터를 찾는 일이 훨씬 복잡해진다.
- 예: (–5, –1)과 (11, 3) 같은 벡터 → 어느 게 shortest인지 직관적으로 알기 어려움.
- 이 때문에 직교 기저가 중요하다.
실제로 격자 기저를 “직교에 가깝게” 바꿔주는 방법으로 Gram–Schmidt 정규화 같은 기법이 중요하게 쓰인다.
📘 기저를 좋게 만드는 과정
👉 Gram–Schmidt 정규화 (실수배 허용)
- 주어진 기저 벡터들을 서로 직교하는 기저로 바꿔주는 방법
- 벡터 $v_2$에서 $v_1$ 방향 성분을 빼주면, $v_1$과 직교하는 새로운 벡터가 된다.
- 이런 식으로 순차적으로 직교 성분을 제거하면, 원래와 같은 공간을 span하는 직교 기저를 얻을 수 있다.
단점: 격자는 정수배만 허용하는데, Gram–Schmidt는 실수배를 쓰므로 격자 안에서는 바로 적용 불가.
- Gram–Schmidt 정규화 (Step-by-Step)
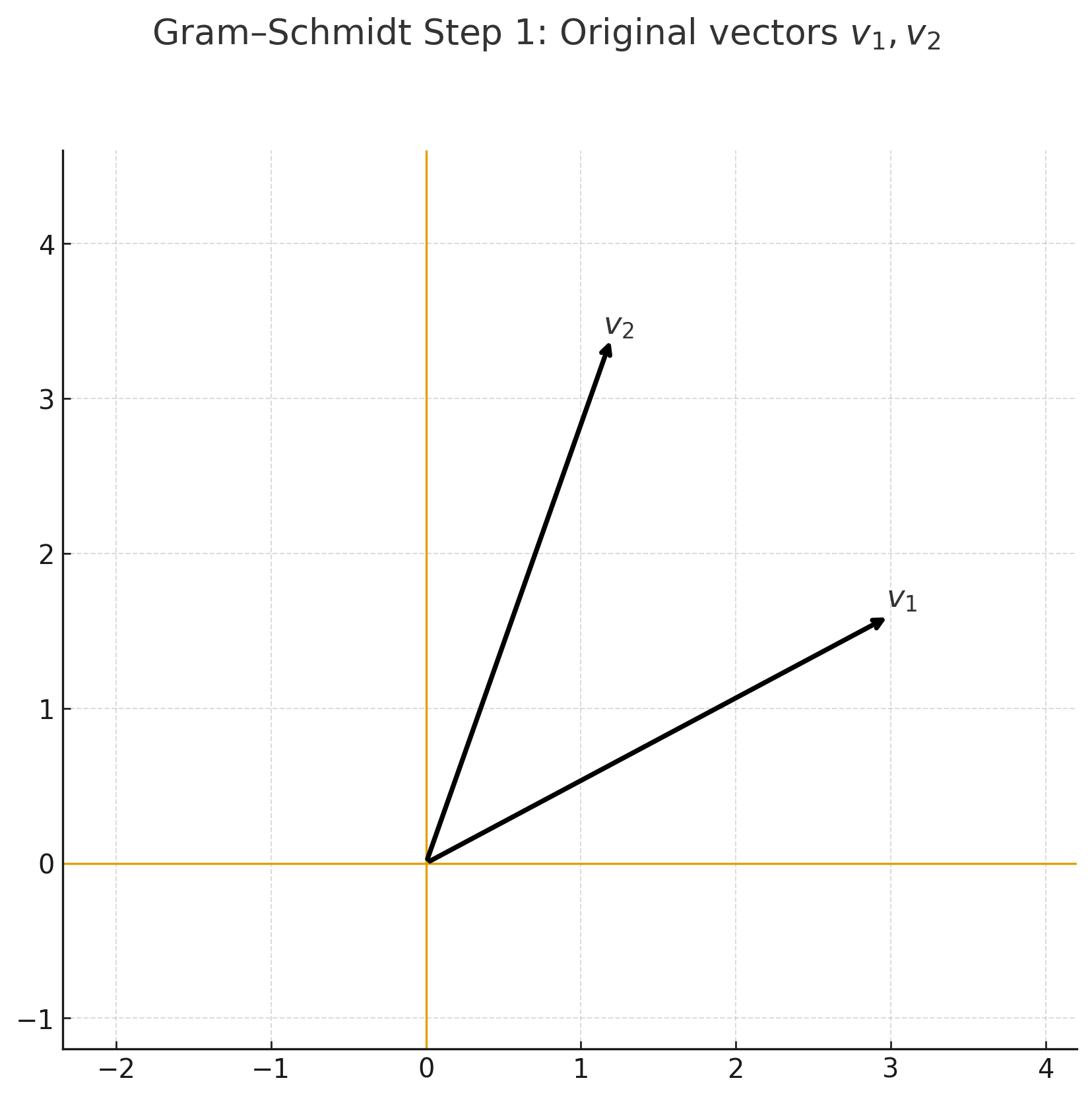 Step 1 — 원래 기저 \(v_1, v_2\) | 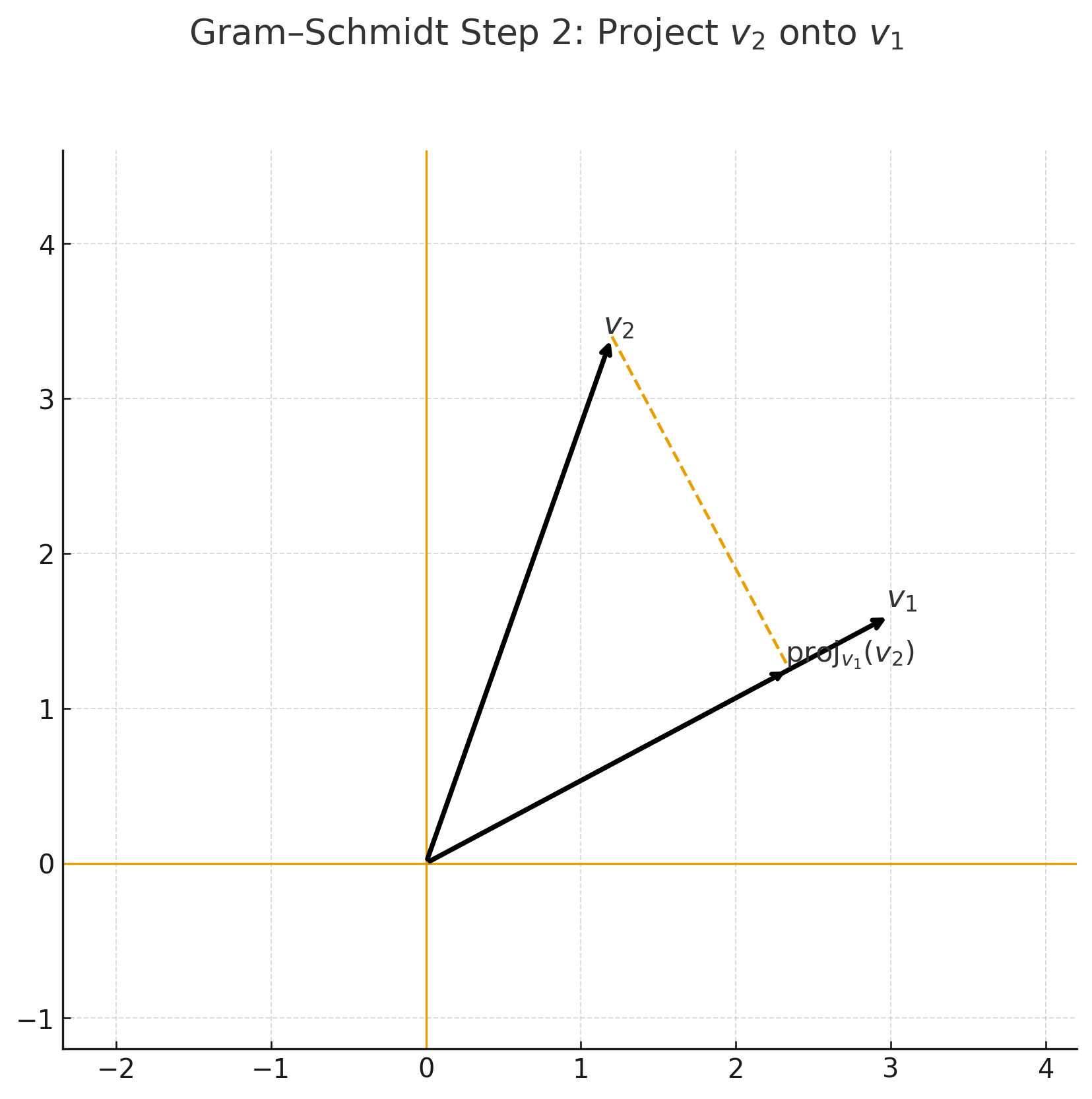 Step 2 — \(v_2\)를 \(v_1\) 위로 정사영 |
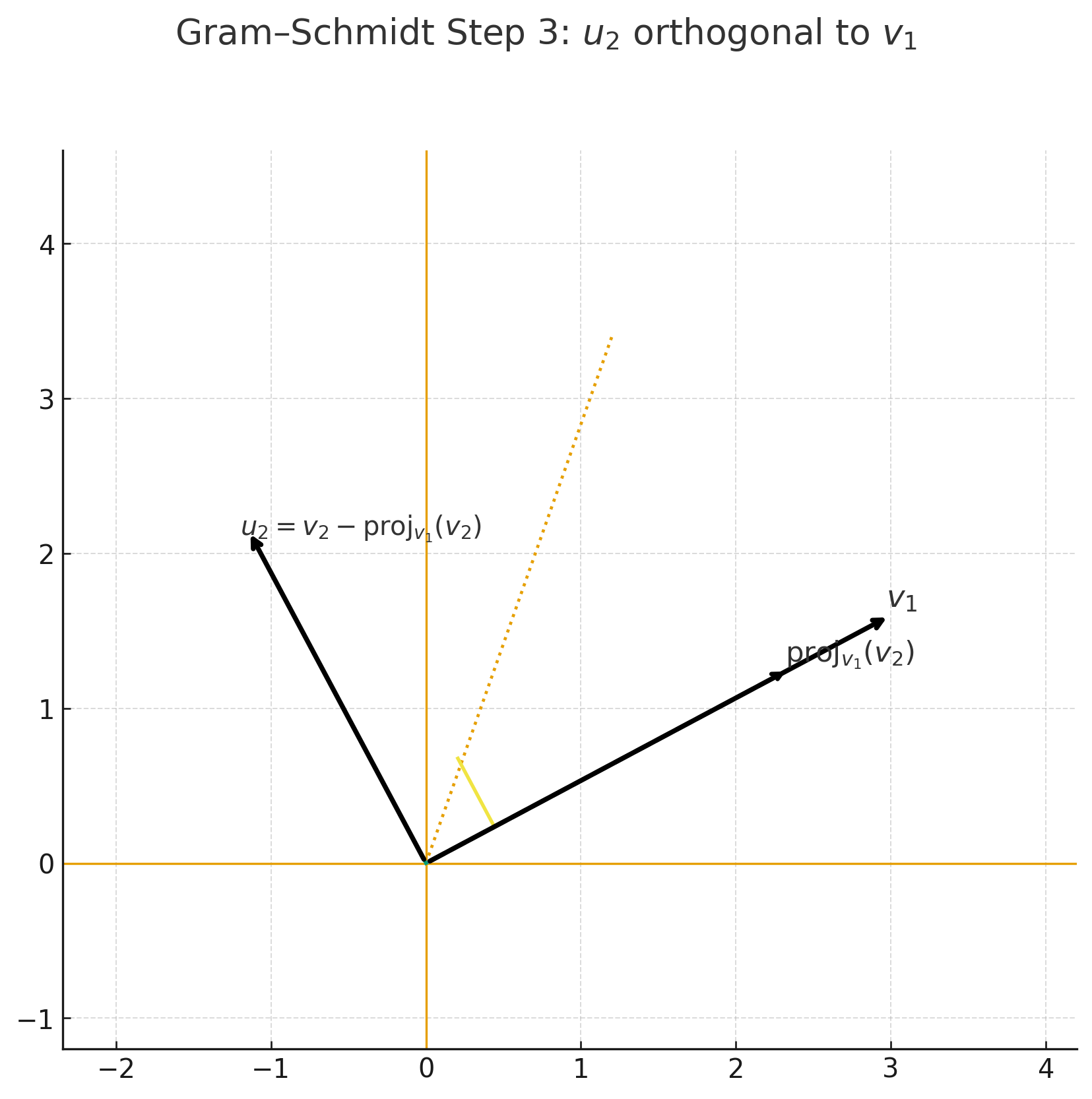 Step 3 — \(u_2 = v_2 - \mathrm{proj}_{v_1}(v_2)\) | 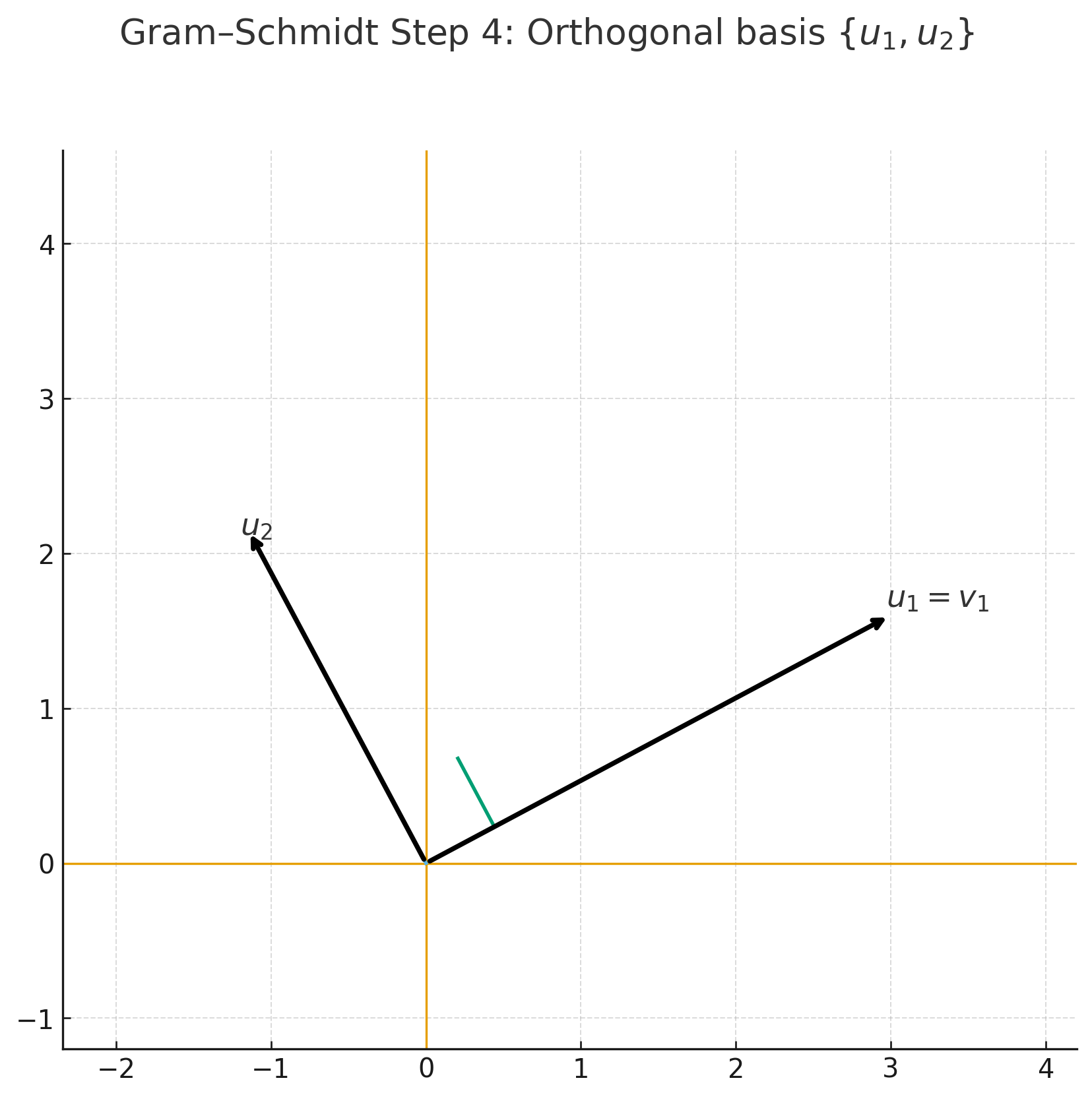 Step 4 — 직교 기저 \(\{u_1, u_2\}\) |
👉 가우스 환원 (정수배만 허용)
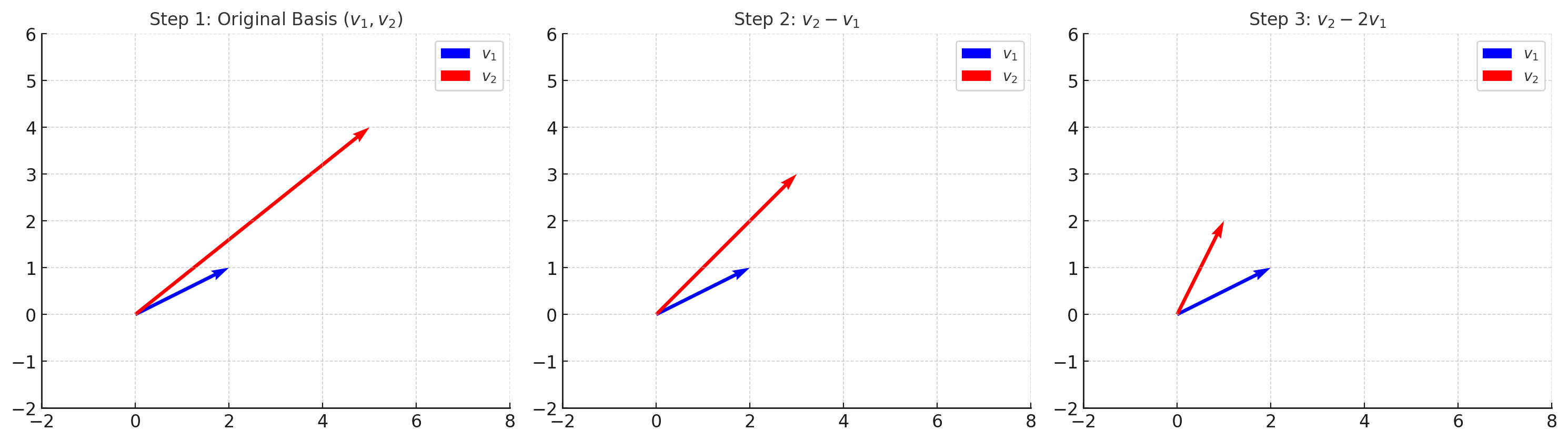
- 격자 기저를 더 수직에 가깝게 만드는 방법.
- $v_2$에서 $v_1$의 정수배를 반복해서 빼주면, 점점 짧고 수직에 가까운 벡터가 만들어진다.
- 이 과정을 번갈아 적용하면, 결국 “더 좋은 기저”를 찾을 수 있다.
- 가우스는 2차원에서 이 환원이 항상 유한 번 안에 끝난다는 것을 증명했다.
👉 차원 확장과 난이도
- 3차원, 4차원에서도 비슷한 아이디어로 기저를 개선할 수 있다.
- 하지만 차원이 커질수록 계산량이 기하급수적으로 증가한다.
- 결국 고차원 격자에서 SVP를 푸는 문제는 NP-hard임이 1997년에 증명되었다.
3) Geometry of Numbers: Lattices (3)
- Hardness of SVP
- SVP는 NP-hard로 알려져 있음 → 고차원 격자에서는 효율적 해법 없음
- 하지만 수학자들은 “격자점의 최소 길이 벡터는 어느 정도일까?”라는 질문을 오래 연구함
📘 Minkowski의 통찰
- 격자의 볼륨 (Det)
- 기저 벡터들이 만드는 평행사변형/평행육면체의 부피는 격자에 대한 불변량이다.
- 기저를 $v_1, v_2$로 잡든, $v_2, v_3$로 잡든 $\det(L)$ 값은 변하지 않는다.
- 직교 기저로 생각해보기
- 만약 $n$차원에서 모든 기저 벡터가 서로 직교하고, 길이가 모두 $\ell$이라면,
\(\det(L) = \ell^n \;\;\Rightarrow\;\; \ell = \det(L)^{1/n}\) - 따라서 최소 벡터의 길이는
\(\lambda_1(L) \leq \det(L)^{1/n}\)
정도일 것이라 직관할 수 있다.
- 만약 $n$차원에서 모든 기저 벡터가 서로 직교하고, 길이가 모두 $\ell$이라면,
- Minkowski의 정리
- 실제 일반 격자에서는 기저가 직교하지 않으므로, 위 직관보다 더 넉넉한 상한이 필요하다.
- Minkowski는 다음을 증명했다:
\(\lambda_1(L) \leq \sqrt{n}\,\det(L)^{1/n}\) - 즉, 최소 벡터의 길이는 격자의 부피(det)와 차원(n)에 의해 제약된다.
- 고차원에서는 $\sqrt{n}$보다 더 좋은 값이 알려진 경우도 있지만, $n \geq 10$ 이상에서는 여전히 정확한 상한이 미해결 문제다.
- 수학 문제를 다루는 세 가지 질문
- Existence (존재성): 해가 존재하는가?
- Uniqueness / Number (유일성·개수): 하나인가, 여러 개인가?
- Computability (계산 가능성): 실제로 계산 가능한가?
📘 LLL 알고리즘
- 배경
- Shortest Vector Problem (SVP)는 NP-hard → “계산 가능성”에 대한 해답이 필요하다.
- 아이디어
- 짧은 벡터를 찾으려면 더 좋은 기저(직교에 가까운 기저)가 필요하다.
- Gram–Schmidt 정규화는 실수 계수를 사용해야 해서 정수 격자에는 그대로 적용 불가
- LLL(1982)은 Gram–Schmidt를 기반으로 하되, projection coefficient \(\mu_{i,j} \;=\; \frac{\langle b_i,\, b_j^* \rangle}{\langle b_j^*,\, b_j^* \rangle}\) 를 계산한 뒤, 이를 가장 가까운 정수로 반올림하여
\(b_i \;\leftarrow\; b_i - \lfloor \mu_{i,j} \rceil \, b_j\) 형태로 기저를 반복 조정한다. - 이렇게 해서 완전히 직교는 아니더라도, 짧고 서로 덜 기울어진(nearly orthogonal) 기저를 구성할 수 있다.
- 결과
- $n$차원 격자에 대해,
\(\|v\| \leq 2^{(n-1)/4}\,\det(L)^{1/n}\)
이하의 길이를 갖는 벡터를 항상 찾을 수 있다. - 특히 낮은 차원($n \leq 17$)에서는 실제 shortest vector까지 정확히 찾아준다.
- $n$차원 격자에 대해,
- 의의
- NP-hard 문제에 대한 최초의 근사 해법.
- 지금도 수학자들이 “아름다운 알고리즘”으로 꼽는다.
- 현대 격자 기반 암호의 안전성 분석과 구현에서 핵심 도구로 활용된다.
- 격자 문제와 암호학
- 1980s: LLL의 등장으로 격자 문제가 “풀릴 수 있다”는 큰 기대
- 1990s: 하지만 $n$이 커지면 근사만 가능, 1996–97년에 SVP, CVP의 NP-hard성 증명
- 이 어려움은 암호학적 전환점이 되었음 → 격자 기반 암호(PQC)의 출발점
- 하지만 초기 격자 암호(예: Knapsack)는 LLL로 쉽게 깨짐
- 이유: NP-hard = 평균적으로 어렵다 는 아님
- 격자는 hard instance는 존재하지만, 대부분은 쉽게 풀림
- 비교:
- 이산로그 문제: self-reducible → 평균적으로 어렵다
- 인수분해 문제: 일반적으론 쉽지만 특수 구조(소수 곱)일 때 어려움 → RSA 기반
- Lattice: hard instance는 있지만 비율이 낮음
4) Geometry of Numbers: Lattices (4)
📘 Ajtai (1996–98): SIS 문제
- SIS (Small Integer Solution) 문제 제안
- 격자 문제 중 처음으로 average-case에서도 어렵다는 사실을 증명
- 즉, 무작위 인스턴스도 본질적으로 어렵다는 걸 보여줌
- 이로써 격자 문제를 기반으로 암호학을 설계할 수 있다는 가능성이 열림
- Regév (2003): LWE (Learning With Errors)
- $b = As + e \pmod{q}$ 꼴의 문제 정의 ($A$: 행렬, $s$: 비밀 벡터, $e$: 작은 에러)
- 에러가 없으면 단순 선형 방정식 → 매우 쉽게 풀림
- 하지만 작은 에러 $e$가 추가되면 문제는 급격히 어려워진다.
- LWE는 worst-case 격자 문제 → average-case LWE 문제로의 reduction이 존재
- 즉, 최악의 경우 어려우면 평균적으로도 어렵다는 것
- 이 reduction은 CVP(Closest Vector Problem) 등과의 연관 속에서 증명됨
- 의의
- Ajtai의 SIS → Regév의 LWE로 이어지며, NP-hard 격자 문제의 난이도가 실제 암호학적 안전성으로 연결됨
- 하지만 초기 LWE 암호는 파라미터(키 사이즈 등)가 너무 커서 실용성이 낮았다.
- 이후 최적화 연구를 거쳐 오늘날 PQC 표준의 기반이 됨
5) PKE from LWE
- 비밀키 암호 (대칭키 관점)
- 키 생성: $s \in \mathbb{Z}_q^n$
- 암호화: \(\text{Enc}_s(m) = (b, \langle b, s \rangle + e + m)\)
- $e$: 작은 노이즈, $m$: 메시지
- $v_i = \langle b_i, s \rangle + e_i$
→ 내적 후 작은 에러를 더해 메시지를 숨긴 것
- 공개키 암호 (Regév, 2005)
- 아이디어: “0의 암호화”를 여러 개 공개 → 그 조합에 $m$을 더해 새로운 암호문 생성
- 성질: $\text{Enc}_s(0) + m = \text{Enc}_s(m)$, 여러 개를 조합해도 여전히 0의 암호문
- 구체적 구성
- 공개키: $B, v = Bs + 2e$
- 암호화: $(c_1, c_2) = (rB, rv + m)$
- 복호화: $c_2 - c_1 s \equiv m + 2re \pmod{q}$
→ 작은 노이즈 무시하고 $m$ 복원
- 한계
- 안전성을 보장하려면 “0의 암호문”을 매우 많이 공개해야 함 (수십만~백만 개)
- 이는 Leftover Hash Lemma로 분석됨
- 초기 LWE 암호는 공개키 크기가 지나치게 커지는 단점이 있었음
📘 Leftover Hash Lemma
- 선형 결합된 분포가 “랜덤 분포와 거의 같다”는 것을 수학적으로 보임
- 기준: 통계적 거리 (Statistical distance ≈ 0)
- 단점: Lemma를 적용하려면 $B$의 크기가 매우 커야 함 (수십만~백만)
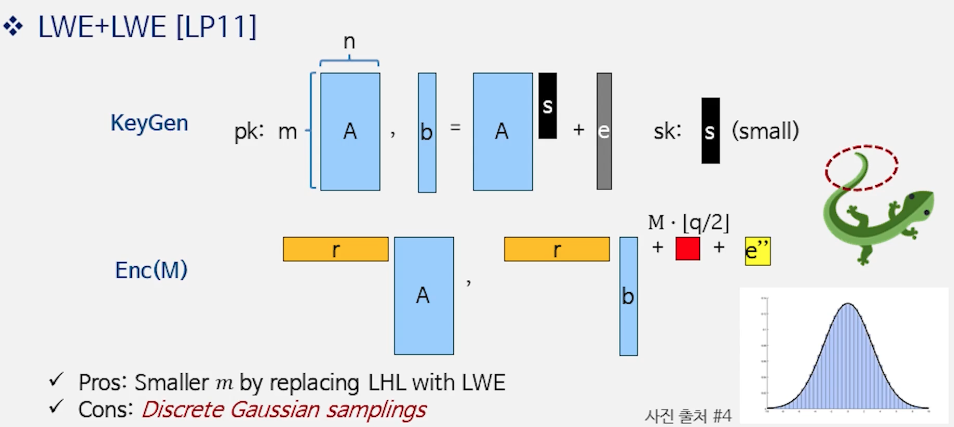
6) LWE + LWE [LP 11]
- 아이디어
- 공개키: $(A, b=As+e)$, 여기서 $e$는 작은 오류(이산 가우시안 등)
암호화: 무작위 $r\in{0,1}^m$로
\[c_1 = rA,\quad c_2 = rb + \left\lfloor \frac{q}{2} \right\rfloor m + e'\]- 문제: $c_1=rA$가 $A$의 행들의 짧은 선형결합이어서, 어떤 행 조합(= $r$)을 썼는지 정보가 새어 나갈 수 있음
- 개선: Lindner–Peikert (2011)
$c_1$에도 추가 잡음 $\hat e$를 주어
\[c_1 = rA + \hat e,\quad c_2 = rb + \left\lfloor \frac{q}{2} \right\rfloor m + e''\]로 만들어, “어느 행을 골랐는가”라는 문제가 다시 LWE-류의 난이도로 귀결되게 설계
핵심 효과: Leftover Hash Lemma (LHL)로 많은 샘플을 공개하지 않고도 작은 $m$으로 안전성 확보
📘 가우시안(이산) 오류와 샘플링
- 증명상 이산 가우시안(또는 서브가우시안) 오류가 표준적 가정
- 예: 표준편차 $\sigma=1$이면 $|X|\le 1\sigma$ 약 68.3%, $2\sigma$ 약 95.5%, $3\sigma$ 약 99.7%
- 구현 난이도: 정확한 이산 가우시안 샘플링은 사전 테이블(CDT/Knuth–Yao) 또는 rejection으로 처리 → 연산/메모리 비용 증가
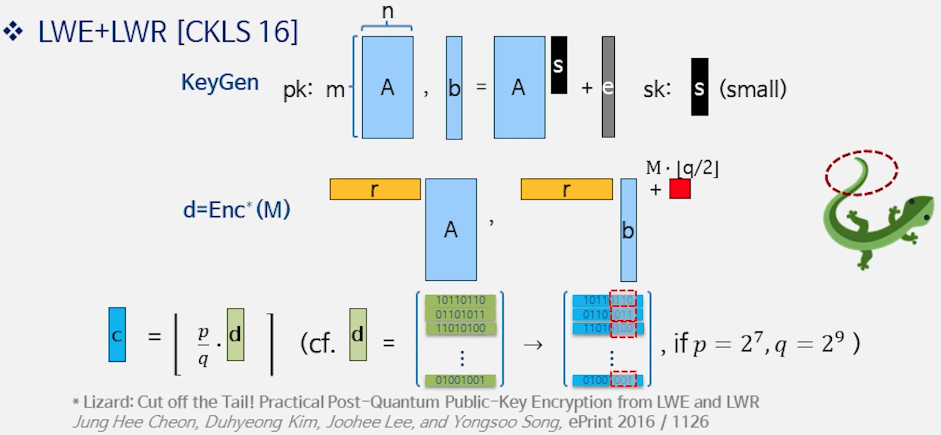
7) LWE + LWR [CKLS 16]
- 후속 아이디어: “Cut off the Tail”
- 관찰: $v_i=\langle b_i,s\rangle+e_i+m$에서, $e_i$가 $k$비트 규모면 하위 $k$비트는 정보가 거의 없다.
→ 하위 비트 truncate(rounding) 로 처리 - 더 나아가, 무작위 노이즈를 따로 샘플링하지 않고 라운딩 자체로 잡음을 유도하는 LWR로 대체
(라운딩은 결정론적이지만, 결과적으로 작은 오차를 주는 효과. $|\mathrm{round}(x)-x|\le q/2^{k+1}$)
- 관찰: $v_i=\langle b_i,s\rangle+e_i+m$에서, $e_i$가 $k$비트 규모면 하위 $k$비트는 정보가 거의 없다.
- 보안/파라미터 직관
- 라운딩만 쓰면 LWE와 분포가 조금 달라져서(carry 등) reduction 경계가 느슨해진다.
→ 이를 보완하려면 더 많이 자르기(큰 $k$) 또는 더 큰 모듈러 $q$가 필요 - 보안은 LWE 난이도에의 리덕션(모듈러스 스위칭 + 라운딩 분석)으로 제공
- 라운딩만 쓰면 LWE와 분포가 조금 달라져서(carry 등) reduction 경계가 느슨해진다.
- 장점
- 가우시안 샘플링 불필요 → 구현 단순화 및 암호화 속도 향상
- 실제 구현에서 키/암호문 크기 대비 효율이 크게 개선
8) Learning with Rounding (LWR) Problem
- 정의
- LWE: $b_i = \langle a_i, s \rangle + e_i \pmod{q}$
- LWR: $b_i = \left\lfloor \tfrac{p}{q} \langle a_i, s \rangle \right\rfloor$
- 작은 노이즈 대신 라운딩(truncation)을 사용
- 핵심 결과
- LWR도 안전함 (LWE로의 reduction 존재)
- 조건: $q$가 충분히 크거나 $m$이 작은 경우
- 구현적으로는 Gaussian 샘플링 없이 효율적
📘 왜 안전한가?
- LWE: “노이즈를 더하고 하위 비트를 버림”
- LWR: “그냥 하위 비트를 버림”
- 두 경우 모두 상위 비트만 정보가 남고 하위 비트는 무의미
- 따라서 안전성이 동일하다고 증명됨
9) Advantages of LWR Assumption
- 기존 LWE 암호화는 ciphertext가 크고, 보안 증명을 위해 가우시안 샘플링이 필요했음
- LWE+LWR(Lizard)에서는 하위 비트를 잘라내는 방식으로 가우시안 샘플링을 제거
- 장점:
- 더 작은 ciphertext
- 더 빠른 암호화 (구현 단순화)
10) Performance & Efficiency
- 격자 기반 암호는 이론적으로 안전성에서 큰 장점을 가지지만,
실제 구현에서는 속도, 키/사이퍼텍스트 크기, 효율성 측면에서 trade-off가 존재한다.
📘 Comparison with RSA and NTRU
- 성능
- 암호화 속도: RSA보다 약 3배 빠름
- 복호화 속도: RSA 대비 200배 이상 빠름 → 실제로 경량화 달성
- Trade-off
- 사이퍼텍스트 크기는 약 2배 커짐
- 타원곡선 기반 암호(ECC)와 비교하면 불리한 점 존재
📘 Recent Implementation
- 성능 개선
- Lizard.CCA: 32-byte 메시지 암호화에 0.020 ms
- RLizard.CCA: 0.036 ms (Category 1, AES-128 수준 양자 보안)
- Key/CT 사이즈
- Lizard.CCA: 공개키 1.8MB (압축 시 0.3MB), CT 0.98KB
- RLizard.CCA: 공개키 4.1KB (압축 시 1.3MB), CT 2.2KB
- 링 구조(RLWE)를 사용하면 더 작은 키 사이즈 가능
- 해석
100k cycles ≈ 0.036 ms(3GHz CPU 기준) → 매우 빠른 연산- Category 1 보안 = AES-128과 동등한 양자 보안 수준
📘 Standardization & Security Margin
- 제안(Proposal)
- 연구팀이 NIST 등 표준화 기구에 알고리즘 사양/코드/보안분석을 제출
- 채택(Selection)
- 여러 후보 중 라운드 진출(1차·2차·3차) 등 표준 후보군으로 선별
- 표준화(Standardization)
- 최종 선정 후 국제/국내 표준 문서로 확정되어 공공·산업에서 공통 사용
- 128비트 보안
- 공격에 대략 $(2^{128}$) 연산이 필요하다는 뜻 (= AES-128급)
- NIST 표현으로는 보통 Category 1 (양자·고전 공격자 모두 고려했을 때 AES-128을 깨는 것과 동일한 난이도) 수준과 대응
- Security Margin(여유분)
- “향후 더 강한 공격”을 대비해 목표 보안보다 여유 비트를 더 줌
- 예: $(128\text{비트} + 10\text{비트}$) 설정 ⇒ 더 큰 파라미터 (키/CT↑)가 필요