Introduction to Homomorphic Encryption
Published: Updated:
해당 포스트는 서울대학교 천정희 교수님의 암호론 강의를 기반으로 작성하였다. 이번 포스트에서는 ‘동형암호의 개요’에 대한 내용을 요약•정리하고자 한다.
동형암호의 개요
1) 동형암호란?
📘 4세대 암호
- 암호화된 상태에서 계산이 가능한 암호로, 키를 갖고 있지 않아도 계산이 가능하다.
→ 키를 보호하는 암호로, 키가 덜 사용된다는 측면에서 키의 안전성이 높은 암호이다.
- 미래 컴퓨팅 환경: 완벽한 하인!
- 우리가 하려는 일의 비밀을 알지 못한 채, 빠르고 정확하게 대신 수행하는 컴퓨터
📘 사례 모음집
- 사례 1: 개인 클라우드 - 데이터를 맡기되, 비밀은 지키기 (대칭키 동형암호)
- 스토리지 클라우드: Dropbox, Google email/calendar, NAS
- 사용자는 데이터를 암호화하여 저장하지만, 클라우드는 복호화 키를 모름
→ 그래도 사용자는 평문처럼 검색하거나 접근 가능함 - 단순한 대칭키 암호는 서버가 데이터를 전혀 활용할 수 없지만, 대칭키 동형암호를 사용하면 암호문 상태에서도 검색·분석이 가능
→ 예: 스팸 필터링, 파일 이름 검색 등
- 사용자는 데이터를 암호화하여 저장하지만, 클라우드는 복호화 키를 모름
- 계산 클라우드: DNA 계산, 헬스케어, 개인성향분석을 통한 추천
- 개인의 민감한 데이터를 암호화한 채 클라우드에 맡겨 계산 가능
- 복호화 키는 오직 데이터 소유자가 보유
→ 이러한 형태의 계산을 대칭키 동형암호라고 함
- 스토리지 클라우드: Dropbox, Google email/calendar, NAS
- 사례 2: 다수 사용자 통계분석 - 데이터를 공유하되, 통제는 유지하기
- 개인정보기반 마케팅 (구글, 페이스북, 네이버 등)
- 사용자의 데이터가 허용된 범위 내에서만 활용되도록 제한 가능
→ 예: 내가 ‘광고에 사용’ 옵션을 허용한 경우에만 마케팅 분석 수행 - 동형암호를 통해 ‘데이터는 사용하되, 직접 보지는 못하게’ 할 수 있음*
- 사용자의 데이터가 허용된 범위 내에서만 활용되도록 제한 가능
- 정부 데이터베이스: 교육, 의료, 납세
- 기관 간 민감 데이터 교류시, 동형암호 기반 연산으로 프라이버시 보장 가능
- 개인정보기반 마케팅 (구글, 페이스북, 네이버 등)
- 동형암호 (Homomorphic Encryption, HE)
- 복호화 없이도 연산이 가능한 암호화 기술, 즉 데이터를 보지 않고도 계산할 수 있는 암호
📘 참고. 영지식 증명 (Zero-Knowledge Proof, ZKP)
- 2017년, 영지식 (Zero-Knowledge) SNARG 계산 증명 기술 등장
- 연산 결과를 직접 공개하지 않고도 “올바르게 계산되었음”을 증명할 수 있음
- 즉, 비밀은 보호하면서도 신뢰를 확보하는 기술
→ 대표 활용: 블록체인 개인정보 보호, 신원 인증, 거래 검증
📘 동형암호의 작동 원리
예를 들어, 우리가 1 + 2라는 단순한 계산을 하고 싶다고 하자. 하지만 계산의 내용을 클라우드에 노출하고 싶지 않다. 이때 우리는 각 값을 암호화하여 클라우드에 보낸다. 예를 들어, 1은 33, 2는 54로 암호화된다.
클라우드는 복호화 키를 전혀 알지 못한 채 단순히 암호문끼리의 덧셈(33 + 54)을 수행한다. 계산 결과로 얻은 87은 여전히 암호화된 상태이며, 우리는 이 값을 받아서 복호화하면 최종적으로 3을 얻는다.
이처럼 동형암호는 단순한 산술 연산뿐만 아니라 영상 처리나 머신러닝 모델 추론과 같은 복잡한 계산에도 확장될 수 있다. 예를 들어, 클라우드에게 두 장의 이미지를 암호화된 상태로 보내 “이 두 이미지가 같은지 비교해 달라”고 요청할 수 있다. 클라우드는 이미지 내용을 직접 보지 않고도 연산을 수행해 결과값만을 사용자에게 반환할 수 있다.

📘 동형암호의 직관적 설명
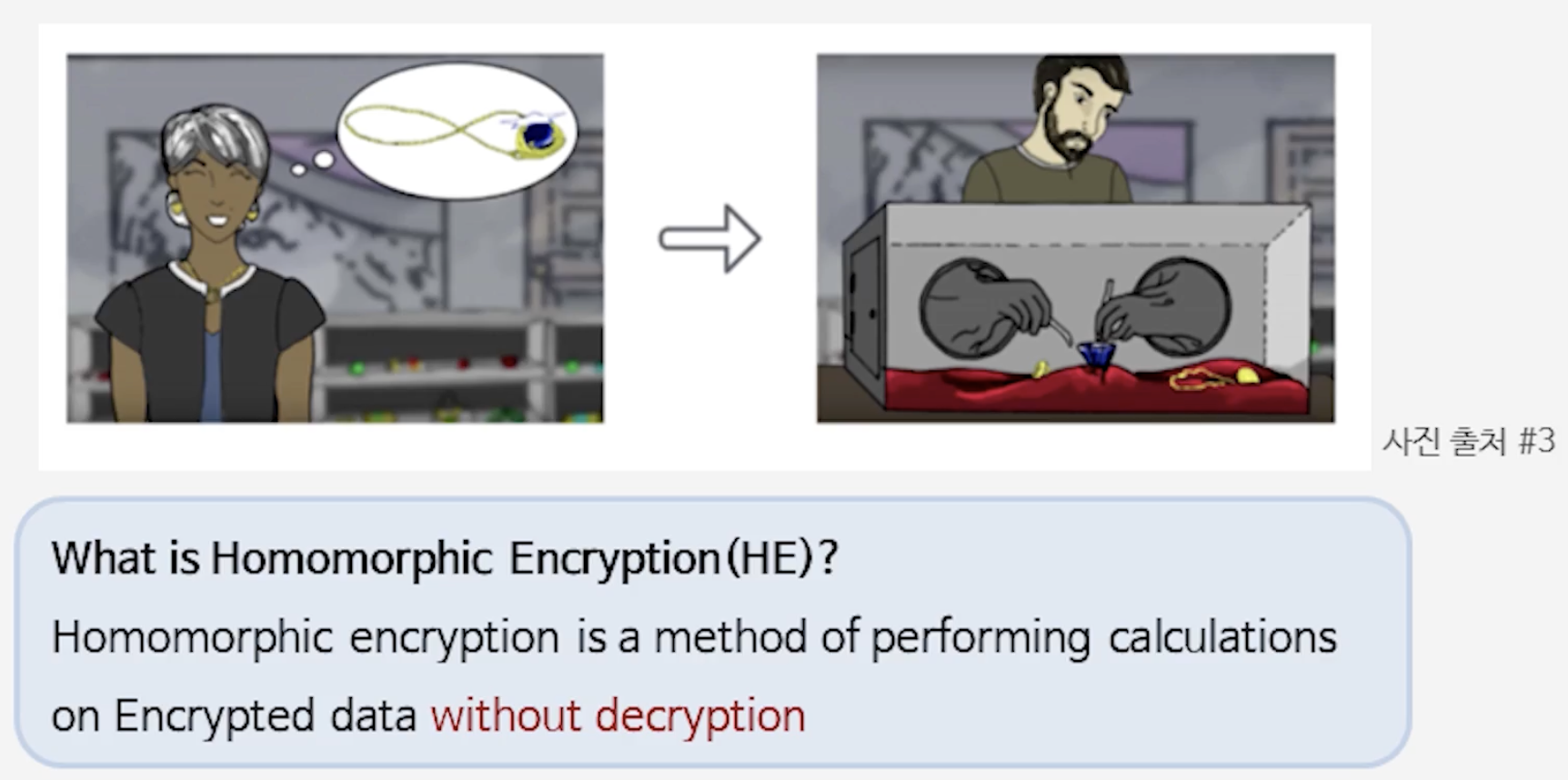
간단한 비유로 설명하면, 전통적인 암호는 열쇠가 있어야만 여는 금고와 같습니다. 키가 없으면 그 안에 무엇이 있는지 전혀 알 수 없고, 아무런 조작도 할 수 없습니다.
반면 동형암호는 “말랑말랑한 금고”와 비슷합니다. 금고 안의 내용(평문)은 외부에서 보이지 않지만, 외부에서 손(연산)을 넣어 내부의 값을 가공할 수 있습니다. 즉, 클라우드(연산자)는 복호화 키를 알지 못한 채도 암호문 위에서 덧셈·곱셈 같은 연산을 수행할 수 있고, 최종 결과는 여전히 암호화된 상태로 반환됩니다. 사용자는 그 결과를 복호화해 실제 정답을 얻습니다.
예시: 의료 데이터의 경우, 환자의 원본 기록은 열리지 않은 상태로 보관됩니다. 연구자는 이 암호화된 데이터를 클라우드에 맡겨 통계분석이나 모델 추론을 수행하게 하고, 클라우드는 내용을 보지 못한 채 계산만 수행합니다. 계산 결과(예: 위험 지표)는 암호화된 상태로 돌아오고, 복호화 권한이 있는 사람만이 필요한 정보(예: 특정 진단의 유무 또는 요약된 수치)만 확인합니다.
핵심은 "비밀은 지키면서도 필요한 계산은 수행할 수 있다"는 점입니다. 이 성질 덕분에 동형암호는 개인정보·의료·금융 데이터의 안전한 외부 계산(클라우드 기반 분석, 암호화된 ML 추론 등)에 유용합니다.
- 동형암호의 장·단점
- 장점: 튜링완전성 (Turing-Complete)
- 암호화된 상태에서 AND, OR, NOT 연산이 모두 가능하다. 즉, 컴퓨터가 수행할 수 있는 모든 연산 (검색·통계처리·머신러닝)을 암호화된 데이터 위에서 수행할 수 있다.
→ 따라서 데이터 유출 위험을 원천 차단할 수 있다.
- 암호화된 상태에서 AND, OR, NOT 연산이 모두 가능하다. 즉, 컴퓨터가 수행할 수 있는 모든 연산 (검색·통계처리·머신러닝)을 암호화된 데이터 위에서 수행할 수 있다.
- 단점
- 암호문 크기 확장: 평문 대비 약 $10$ ~ $100K$배 (대칭키 방식은 약 $0.1$ ~ $1K$ 배 수준)
- 암·복호화 속도 저하: AES ≈ $1 us$, RSA ≈ $1 ms$, HE ≈ 수십 $ms$
- 암호문 연산 속도 저하: 특히 곱셈 연산은 평문 계산 대비 수백 배 이상 느림
- 응용별 성능 편차: 연산의 종류 (덧셈·곱셈·비교)에 따라 속도 차이가 크며, 효율을 높이기 위해 개별 최적화 알고리즘 및 구현 기술이 필요함
📘 예시 (복잡도 관점의 단순 모델)
- 128-bit 보안을 만족하기 위해 키 크기를 50배 늘린다고 가정하면, 계산량은 일반적으로
O(n^2)복잡도를 가지므로 $50^2x = 2,500x$ 배 증가하게 된다.- 그러나 빠른 곱셈 알고리즘 (Fast Multiplication)을 적용하면 복잡도는
O(nlog n)수준으로 개선되어 $(50 \log 50)x ≈ 2,000x$ 정도로 줄어든다.👉 따라서, 키 길이를 $50$배 늘려도 계산량은 약 $2,000$배 증가하게 된다. 즉, 보안 강도를 높이는 것은 필연적으로 연산 비용 증가를 수반한다.
- 물론 위 계산은 최적화가 잘 이루어진 경우를 가정한 것이다. 실제로는 알고리즘과 구현 수준에 따라 성능 편차가 크며, 이러한 최적화(optimization)는 인공지능이 아니라 사람이 직접 설계해야 한다. 다시 말해, 알고리즘적·구현적 튜닝이 부족한 경우에는 여전히 수천 배에서 수만 배까지 느린 사례도 존재한다.
- 장점: 튜링완전성 (Turing-Complete)
2) 동형암호의 종류
- 정수 기반 동형암호 (Integer-based HE scheme)
동형암호의 초기 형태는 **정수 연산 기반**으로 설계되었습니다. 대표적으로 RAD PH와 DGHV 스킴이 있습니다.
- RAD PH Scheme
- 키 생성
- Secret Key: large prime $p$
- Public Key: $n = p q_0$
- 암호화 (Encryption) : $Enc(m) = m + p q \pmod{n}$
- 복호화 (Decryption) : $Enc(m) \bmod p = m$
덧셈 연산
\(Enc(m_1) + Enc(m_2) = (m_1 + p q_1) + (m_2 + p q_2) = (m_1 + m_2) + p(q_1 + q_2) = Enc(m_1 + m_2)\)- ✅ 결과:
평문 덧셈이 암호문 덧셈으로 보존되므로 부분동형(ADD-homomorphic) 속성을 가진다.
그러나 INSECURE — 잡음(noise) 누적과 키 복원 공격에 취약하다.
- 키 생성
- DGHV HE scheme (on $\mathbb{Z}_{2}$)
- 암호화 : $Enc(m) = m + 2e + p q$
- $m \in {0,1}$: 메시지 비트
- $e$: 작은 노이즈 (error term)
- $p, q$: 큰 정수
- 특징
- 양자 컴퓨팅에 대해 안전 (Post-Quantum Secure)
- 정수 기반 대신 다항식 링 구조를 사용하는 고도화된 확장 버전 존재:
$R_q = \mathbb{Z}_q[x] / (x^n + 1)$
- ✅ 의의:
DGHV는 Craig Gentry의 Fully Homomorphic Encryption (FHE)의
초기 형태로, “잡음을 제어하며 연산을 확장하는” 아이디어의 기반이 되었다.
- 암호화 : $Enc(m) = m + 2e + p q$
</div>
- RAD PH Scheme
</details>