I. Basic Math: A-1. Modulo Arithmetic
Published:
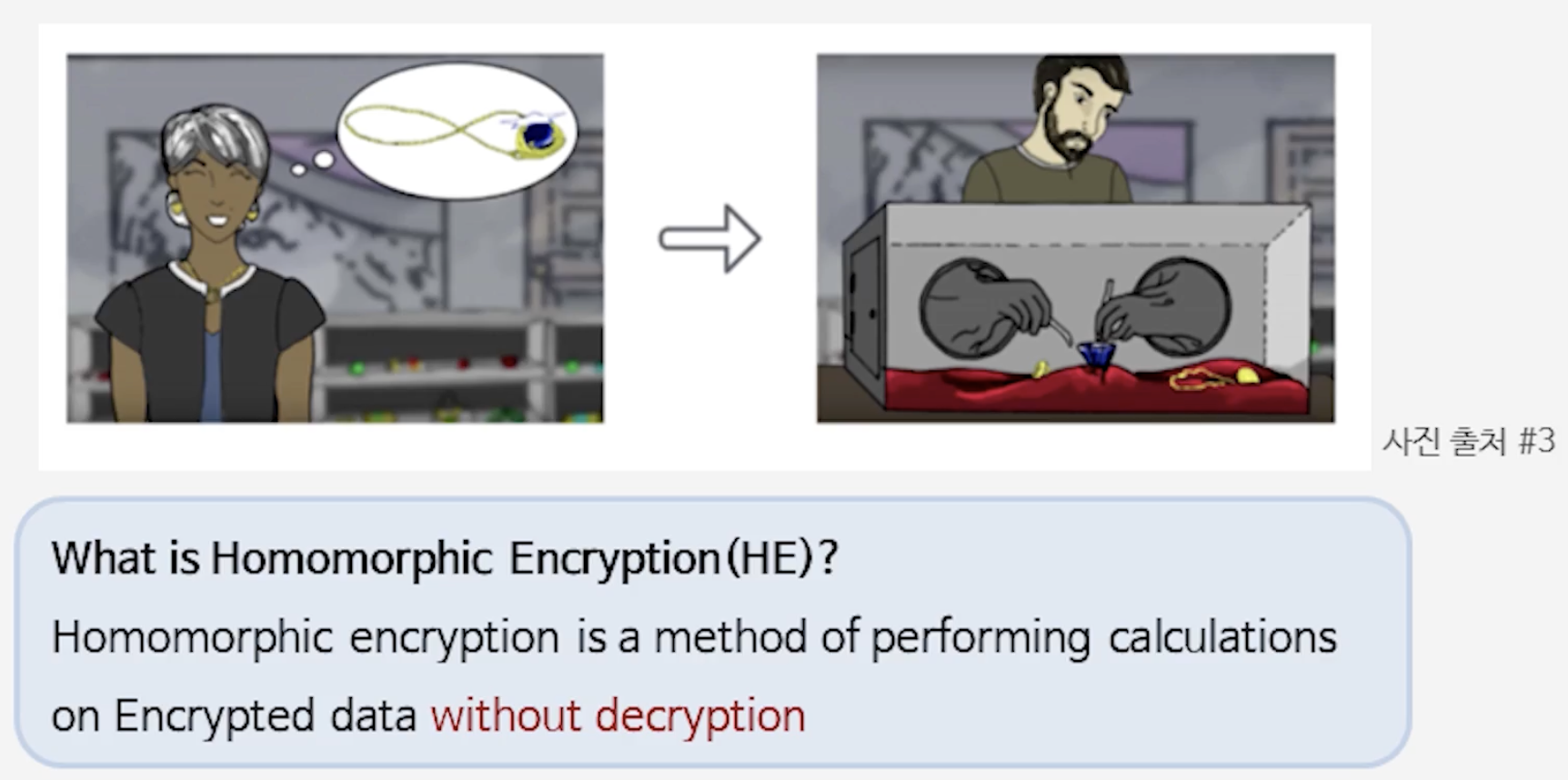
해당 포스트는 Ronny Ko의 저서 The Beginner’s Textbook for Fully Homomorphic Encryption을 기반으로 작성하였다. 이번 포스트에서는 ‘I. Basic Math: A-1. Modulo Arithmetic’ 파트를 요약•정리하고자 한다.
A-1. Modulo Arithmetic (모듈러 산술)
1) Overview
Reference: Extended Euclidean Algorithm Tutorial
- 모듈러 (modulo, mod) 란, 한 수를 다른 수로 나눌 때 나머지를 계산하는 연산을 의미한다.
- 수식으로 표현하면 다음과 같다: \(A = BQ + R\)
- $A$: 피제수 (dividend), $B$: 제수 (divisor)
- $Q$: 몫 (quotient), $R$: 나머지 (remainder)
→ 따라서, “$A \bmod B = R$” 혹은 “$A$ modulo $B = R$” 로 표현할 수 있다.
- 수식으로 표현하면 다음과 같다: \(A = BQ + R\)
- $a \bmod q$ ( i.e., $a$ modulo $q$ ): $a$를 $q$로 나눈 나머지를 의미한다.
이때 나머지는 항상 $({0, 1, 2, 3, …, q-1})$ 사이의 값이다.- 예: $7 \bmod 5 = 2$
모듈러스 (modulus): $a \bmod q$가 주어졌을 때, divisor q를 모듈러스라 부른다.
반면, 모듈러 (modulo)는 연산(operation) 자체를 의미한다.- 모듈러 합동식 (Modulo Congruence): 두 정수 $a, b$가 $q$로 나눴을 때 같은 나머지를 가지면, $a$는 $b$와 모듈러스 $q$에 대해 합동이다.
\(a \equiv b \bmod q ⟺ a = b \pmod q\)- 예) $5 \equiv 12 \bmod 7$
- $5 \bmod 7 = 12 \bmod 7 = 5$
- 주의: $b$를 $q$로 나누었을 때 나머지 $a$를 뜻하는 $a = b \bmod q$ 식과는 다르다.
- 예) $5 \equiv 12 \bmod 7$
- 합동식 vs 동치 (Congruence vs Equality):
임의의 정수 $k$에 대해서,
\(a \equiv b \bmod q ⟺ a = b + k \cdot q\)
→ 즉, $a$와 $b$는 $q$의 정수배만큼 차이가 있을 때, 모듈러스 $q$에 대해 서로 합동이다.- 예) $5 \equiv 12 \bmod 7 ⟺ 5 = 12 + (-1) \cdot 7$
2) 모듈러 산술 (Modulo Arithmetic)
- 모든 정수 $x$에 대해서, 다음이 성립한다:
- Addition (덧셈): $a \equiv b \bmod q ⟺ a + x \equiv b + x \bmod q$
- Subtraction (뺄셈): $a \equiv b \bmod q ⟺ a - x \equiv b - x \bmod q$
- Multiplication (곱셈): $a \equiv b \bmod q ⟺ a \cdot x \equiv b \cdot x \bmod q$
📘 Proof (증명)
모든 정수 $x$에 대하여 다음이 성립한다:
Addition (덧셈):
$a \equiv b \bmod q$ ⟺ $a = b+kq$ (임의의 $k$에 대해) # 이때 $a, b$는 $q$의 배수 차이를 가짐
⟺ $a + x = b+k \cdot q + x$
⟺ $a + x = b+x + k \cdot q$ # $a + x, b + x$는 $q$의 배수 차이를 가짐
⟺ $a + x \equiv b + x \bmod q$Subtraction (뺄셈):
$a \equiv b \bmod q$ ⟺ $a = b+kq$ (임의의 $k$에 대해)
⟺ $a - x = b+k \cdot q - x$
⟺ $a - x = b-x + k \cdot q$ # $a - x, b - x$는 $q$의 배수 차이를 가짐
⟺ $a - x \equiv b - x \bmod q$Multiplication (곱셈):
$a \equiv b \bmod q$ ⟺ $a = b+kq$ (임의의 $k$에 대해)
⟺ $a \cdot x = b+k \cdot q \cdot x$
⟺ $a \cdot x = b \cdot x + k_{x} \cdot q$ ($k_{x}=k \cdot x$ 일 때)# $a \cdot x, b \cdot x$는 $q$의 배수 차이를 가짐
⟺ $a \cdot x \equiv b \cdot x \pmod q$
- Associative (결합법칙): $(a \cdot b) \cdot c \equiv a \cdot (b \cdot c) \bmod q$
- Commutative (교환법칙): $(a \cdot b) \equiv (b \cdot a) \bmod q$
- Distributive (분배법칙): $(a \cdot (b+c)) \equiv ((a \cdot b) + (a \cdot c)) \bmod q$
- Interchangeable (치환 가능성): 모듈러 산술에서는 합동 관계에 있는 값 (congruent values) 은 연산에서 서로 자유롭게 치환 가능하다.
- $(a \equiv b \bmod q)$와 $(c \equiv d \bmod q)$일 경우, 다음이 모두 성립한다:- $(a+c) \equiv (b+d) \equiv (a+d) \equiv (b+c) \bmod q$
- $(a-c) \equiv (b-d) \equiv (a-d) \equiv (b-c) \bmod q$
- $(a \cdot c) \equiv (b \cdot d) \equiv (a \cdot d) \equiv (b \cdot c) \bmod q$
모듈러 $q$ (즉, 모든 수를 $q$로 나눈 나머지의 세계)에서, 각 $a in {0, 1, 2, …, q-1}$에 대해 다음과 같이 정의된다.
Additive Inverse (덧셈 역원): $a_{+}^{-1}$은 다음을 만족하는 수이다.
\(a + a_{+}^{-1} \equiv 0 \bmod q\)
- 예. 모듈러 $11$에서 $3_{+}^{-1}=8$ → 왜냐하면 $3 + 8 \equiv 0 \bmod 11$이기 때문이다.Multiplicative Inverse (곱셈 역원): $a_{*}^{-1}$은 다음을 만족하는 수이다.
\(a \cdot a_{\*}^{-1} \equiv 1 \bmod q\)
- 예. 모듈러 $11$에서 $3_{*}^{-1}=4$ → 왜냐하면 $3 \cdot 4 \equiv 1 \bmod 11$이기 때문이다.
- Modulo Division (모듈러 나눗셈)
- 모듈러 산술에서의 나눗셈은 일반적인 수학적 나눗셈과는 다르다. (엄밀히 말하면, 모듈러 나눗셈은 존재하지 않는다.) 왜냐하면 모듈러 연산 자체가 이미 나머지를 구하는 일종의 나눗셈이기 때문이다.
하지만 어떤 수 $b$를 $a$로 “모듈러 나누기” 하고자 한다면, 이는 곧 $a$의 모듈러 역원 (modular inverse)을 이용한 곱셈으로 표현할 수 있다. \(b \div a \bmod q \; \equiv \; b \cdot a_{*}^{-1} \bmod q\)
즉, 모듈러 나눗셈(modulo division)은 모듈러 곱셈 (modulo multiplication)으로 정의된다.📍 중요한 차이점:
- 일반적인 나눗셈은 실수(real number)를 결과로 내지만,
모듈러 나눗셈은 항상 정수(integer)를 결과로 낸다.
(이는 $b$와 $a_{*}^{-1}$ 모두 정수이기 때문)
- 일반적인 나눗셈은 실수(real number)를 결과로 내지만,
- 마지막으로, 정수 $a$의 모듈러 역원은 확장 유클리드 알고리즘 (Extended Euclidean Algorithm)을 이용해 계산할 수 있다.
- 중심 잔여 표현 (Centered Residue Representation)
Canonical은 0부터 시작하는 잔여계, Centered는 0을 기준으로 대칭인 잔여계다
지금까지 잔여(나머지, Residue)를 양의 정수(positive integer)라고 가정했다.
모듈러 $q$에서 가능한 나머지 집합은 다음과 같다.
\({0, 1, 2, \dots q-1}\)→ 이 표현 방식을 표준 잔여계(canonical residue system) 또는 비부호형 잔여 표현 (unsigned residue representation) 이라고 부른다.
🔸 하지만 또 다른 표현 방식도 존재한다.
바로 부호형 잔여계 (signed or centered residue system) 로, 잔여들이 0을 중심으로 대칭되게 분포한다. \({-\frac{q}{2}, -frac{q}{2}+1, \dots, 0, \dots, frac{q}{2}-2, \frac{q}{2}-1}\)→ 비부호형 잔여계나 부호형 잔여계 모두 잔여의 개수는 동일하게 $q$개이다. 차이는 단지 잔여 범위의 기준점(upper/lower bound)에 있다.
표현 방식 잔여 집합 하한(lower bound) 상한(upper bound) Canonical (Unsigned) $\{0, 1, 2, \dots, q-1\}$ 0 $q-1$ Centered (Signed) $\{-\frac{q}{2}, \dots, 0, \dots, \frac{q}{2}-1\}$ $-\frac{q}{2}$ $\frac{q}{2}-1$ 💡 모듈러 연산의 역할
모듈러 연산은 주어진 값을 위 두 시스템 중 하나의 잔여 범위로 변환한다.- 값이 상한보다 크면 → 모듈러스 $q$를 빼준다
- 값이 하한보다 작으면 → 모듈러스 $q$를 더해준다
→ 따라서 두 시스템의 차이는 단지 잔여의 “표현 방식”일 뿐, 모두 동일한 모듈러 집합 $\mathbb{Z}_q$를 나타낸다.
\[\mathbb{Z}_q = \{0, 1, 2, \dots, q - 1\}\]
Canonical과 Centered 잔여계는 모든 연산 성질이 동일하게 유지된다.
표준 잔여계(canonical system)와 중심 잔여계(centered system)는 덧셈 $\cdot$ 뺄셈 $\cdot$ 곱셈 $\cdot$ 나눗셈의 모든 모듈러 성질은 동일하게 성립한다.
\[(a \pm b) \bmod q, \quad (a \times b) \bmod q, \quad (a \div b) \bmod q\]→ 이들이 어떤 잔여계에서 계산되든 결과의 동치 관계는 변하지 않는다.
💡 이유:
두 시스템 모두 같은 모듈러스 $q$를 사용하기 때문에,
어떤 두 동치 잔여(congruent residues)라도 서로 $kq$의 차이를 가진다.
즉,
\(a \equiv b \pmod q \quad \Rightarrow \quad a - b = kq \quad (k \in \mathbb{Z})\)→ 따라서 canonical 표현이든 centered 표현이든, 각 연산의 결과는 항상 같은 동치류(congruence class)에 속하게 된다.
Canonical과 Centered 잔여계의 연산 성질 중 역원도 동일하게 유지된다.
모듈러 $q$에서 $a$의 역원은 다음을 만족한다.
\[a \cdot a^{-1} \equiv 1 \pmod q\]🔹 부호형(signed) 잔여 표현을 사용하는 이유는 특정 상황에서 모듈러 연산을 생략할 수 있을 정도로 계산을 단순화할 수 있기 때문이다.
#### 🧩 예제 1. Canonical (Unsigned) Representation 표준 잔여계에서는
\[(a + b) \bmod q = a + b\]
\((a + b) \bmod q\) 의 형태를 가정하자.
만약 어떤 애플리케이션에서 항상 $0 \le a + b \le q - 1$ 이라는 조건이 보장된다면,따라서 모듈러 연산을 생략할 수 있다.
(즉, 값이 잔여 범위 $[0, q-1]$를 벗어나지 않기 때문)#### 🧩 예제 2. Centered (Signed) Representation 이번에는 중심 잔여계에서
\[(a - b) \bmod q = a - b\]
\((a - b) \bmod q\) 를 생각하자.
만약 $a - b$가 항상 $[-\frac{q}{2}, \frac{q}{2} - 1]$ 범위 안에 있다면,이때도 모듈러 연산을 생략할 수 있다.
#### ⚠️ 주의: Canonical 표현에서의 뺄셈 만약 위와 같은 $(a - b) \bmod q$ 연산을 canonical 표현으로 계산한다면,
$a - b$가 음수일 경우 그 값은 하한(0)보다 작아진다.
이 경우 모듈러스 $q$를 하나 이상 더해주는(modulo reduction) 보정이 필요하다.예를 들어,
\(a = 3, \quad b = 7, \quad q = 11\)
이면
\((a - b) \bmod 11 = (3 - 7) \bmod 11 = (-4) \bmod 11 = 7\)✅ 정리:
- canonical 표현: 음수가 되면 반드시 모듈러 보정 필요
- centered 표현: ±범위 안이면 모듈러 보정 없이 연산 가능
즉, 부호형(centered) 잔여 표현은 덧셈보다 뺄셈 연산에서 더 직관적이며 효율적이다.
§D-5.8 절에서는 centered residue representation의 유리한 성질을 활용하여 FastBConvEx 연산(Fast Balanced Convolution Extension) 을 설계한다.
- 이 알고리즘에서는 다음과 같은 관계가 성립한다.
일반적으로는 모듈러 연산이 필요하지만,
\[-\frac{b^{\alpha}}{2} \leq \mu + u < \frac{b^{\alpha}}{2}\]
이때 $\mu + u$가 항상 centered residue 범위 내에 존재함이 보장된다.따라서, \((\mu + u) \bmod b^{\alpha} = \mu + u\)
즉, 모듈러 연산을 생략하고 단순 덧셈으로 표현할 수 있다.
이는 연산을 간소화하고 계산 효율을 높이는 핵심 아이디어이다.💡 핵심 포인트:
- centered residue 표현을 사용하면,
값이 잔여 범위를 벗어나지 않는 한 모듈러 처리가 불필요하다. - 이 특성은 고속 암호 연산(예: FastBConvEx) 설계 시
불필요한 나머지 계산을 제거하여 성능을 최적화하는 데 사용된다.
</div>
</details>