Sitemap
A list of all the posts and pages found on the site. For you robots out there, there is an XML version available for digesting as well.
Pages
Posts
Homomorphic Encryption - HEaaN
Published:
I. Basic Math: A-3. Field
Published:
해당 포스트는 Ronny Ko의 저서 The Beginner’s Textbook for Fully Homomorphic Encryption을 기반으로 작성하였다. 이번 포스트에서는 ‘I. Basic Math: A-3. Field’ 파트를 요약•정리하고자 한다.
A-3. Field
To be continued …
I. Basic Math: A-2. Group
Published:
해당 포스트는 Ronny Ko의 저서 The Beginner’s Textbook for Fully Homomorphic Encryption을 기반으로 작성하였다. 이번 포스트에서는 ‘I. Basic Math: A-2. Group’ 파트를 요약•정리하고자 한다.
A-2. Group
To be continued …
I. Basic Math: A-1. Modulo Arithmetic
Published:
해당 포스트는 Ronny Ko의 저서 The Beginner’s Textbook for Fully Homomorphic Encryption을 기반으로 작성하였다. 이번 포스트에서는 ‘I. Basic Math: A-1. Modulo Arithmetic’ 파트를 요약•정리하고자 한다.
A-1. Modulo Arithmetic (모듈러 산술)
1) Overview
Reference: Extended Euclidean Algorithm Tutorial
- 모듈러 (modulo, mod) 란, 한 수를 다른 수로 나눌 때 나머지를 계산하는 연산을 의미한다.
- 수식으로 표현하면 다음과 같다: \(A = BQ + R\)
- $A$: 피제수 (dividend), $B$: 제수 (divisor)
- $Q$: 몫 (quotient), $R$: 나머지 (remainder)
→ 따라서, “$A \bmod B = R$” 혹은 “$A$ modulo $B = R$” 로 표현할 수 있다.
- 수식으로 표현하면 다음과 같다: \(A = BQ + R\)
- $a \bmod q$ ( i.e., $a$ modulo $q$ ): $a$를 $q$로 나눈 나머지를 의미한다.
이때 나머지는 항상 $({0, 1, 2, 3, …, q-1})$ 사이의 값이다.- 예: $7 \bmod 5 = 2$
모듈러스 (modulus): $a \bmod q$가 주어졌을 때, divisor q를 모듈러스라 부른다.
반면, 모듈러 (modulo)는 연산(operation) 자체를 의미한다.- 모듈러 합동식 (Modulo Congruence): 두 정수 $a, b$가 $q$로 나눴을 때 같은 나머지를 가지면, $a$는 $b$와 모듈러스 $q$에 대해 합동이다.
\(a \equiv b \bmod q ⟺ a = b \pmod q\)- 예) $5 \equiv 12 \bmod 7$
- $5 \bmod 7 = 12 \bmod 7 = 5$
- 주의: $b$를 $q$로 나누었을 때 나머지 $a$를 뜻하는 $a = b \bmod q$ 식과는 다르다.
- 예) $5 \equiv 12 \bmod 7$
- 합동식 vs 동치 (Congruence vs Equality):
임의의 정수 $k$에 대해서,
\(a \equiv b \bmod q ⟺ a = b + k \cdot q\)
→ 즉, $a$와 $b$는 $q$의 정수배만큼 차이가 있을 때, 모듈러스 $q$에 대해 서로 합동이다.- 예) $5 \equiv 12 \bmod 7 ⟺ 5 = 12 + (-1) \cdot 7$
2) 모듈러 산술 (Modulo Arithmetic)
- 모든 정수 $x$에 대해서, 다음이 성립한다:
- Addition (덧셈): $a \equiv b \bmod q ⟺ a + x \equiv b + x \bmod q$
- Subtraction (뺄셈): $a \equiv b \bmod q ⟺ a - x \equiv b - x \bmod q$
- Multiplication (곱셈): $a \equiv b \bmod q ⟺ a \cdot x \equiv b \cdot x \bmod q$
📘 Proof (증명)
모든 정수 $x$에 대하여 다음이 성립한다:
Addition (덧셈):
$a \equiv b \bmod q$ ⟺ $a = b+kq$ (임의의 $k$에 대해) # 이때 $a, b$는 $q$의 배수 차이를 가짐
⟺ $a + x = b+k \cdot q + x$
⟺ $a + x = b+x + k \cdot q$ # $a + x, b + x$는 $q$의 배수 차이를 가짐
⟺ $a + x \equiv b + x \bmod q$Subtraction (뺄셈):
$a \equiv b \bmod q$ ⟺ $a = b+kq$ (임의의 $k$에 대해)
⟺ $a - x = b+k \cdot q - x$
⟺ $a - x = b-x + k \cdot q$ # $a - x, b - x$는 $q$의 배수 차이를 가짐
⟺ $a - x \equiv b - x \bmod q$Multiplication (곱셈):
$a \equiv b \bmod q$ ⟺ $a = b+kq$ (임의의 $k$에 대해)
⟺ $a \cdot x = b+k \cdot q \cdot x$
⟺ $a \cdot x = b \cdot x + k_{x} \cdot q$ ($k_{x}=k \cdot x$ 일 때)# $a \cdot x, b \cdot x$는 $q$의 배수 차이를 가짐
⟺ $a \cdot x \equiv b \cdot x \pmod q$
- Associative (결합법칙): $(a \cdot b) \cdot c \equiv a \cdot (b \cdot c) \bmod q$
- Commutative (교환법칙): $(a \cdot b) \equiv (b \cdot a) \bmod q$
- Distributive (분배법칙): $(a \cdot (b+c)) \equiv ((a \cdot b) + (a \cdot c)) \bmod q$
- Interchangeable (치환 가능성): 모듈러 산술에서는 합동 관계에 있는 값 (congruent values) 은 연산에서 서로 자유롭게 치환 가능하다.
- $(a \equiv b \bmod q)$와 $(c \equiv d \bmod q)$일 경우, 다음이 모두 성립한다:- $(a+c) \equiv (b+d) \equiv (a+d) \equiv (b+c) \bmod q$
- $(a-c) \equiv (b-d) \equiv (a-d) \equiv (b-c) \bmod q$
- $(a \cdot c) \equiv (b \cdot d) \equiv (a \cdot d) \equiv (b \cdot c) \bmod q$
모듈러 $q$ (즉, 모든 수를 $q$로 나눈 나머지의 세계)에서, 각 $a in {0, 1, 2, …, q-1}$에 대해 다음과 같이 정의된다.
Additive Inverse (덧셈 역원): $a_{+}^{-1}$은 다음을 만족하는 수이다.
\(a + a_{+}^{-1} \equiv 0 \bmod q\)
- 예. 모듈러 $11$에서 $3_{+}^{-1}=8$ → 왜냐하면 $3 + 8 \equiv 0 \bmod 11$이기 때문이다.Multiplicative Inverse (곱셈 역원): $a_{*}^{-1}$은 다음을 만족하는 수이다.
\(a \cdot a_{\*}^{-1} \equiv 1 \bmod q\)
- 예. 모듈러 $11$에서 $3_{*}^{-1}=4$ → 왜냐하면 $3 \cdot 4 \equiv 1 \bmod 11$이기 때문이다.
- Modulo Division (모듈러 나눗셈)
- 모듈러 산술에서의 나눗셈은 일반적인 수학적 나눗셈과는 다르다. (엄밀히 말하면, 모듈러 나눗셈은 존재하지 않는다.) 왜냐하면 모듈러 연산 자체가 이미 나머지를 구하는 일종의 나눗셈이기 때문이다.
하지만 어떤 수 $b$를 $a$로 “모듈러 나누기” 하고자 한다면, 이는 곧 $a$의 모듈러 역원 (modular inverse)을 이용한 곱셈으로 표현할 수 있다. \(b \div a \bmod q \; \equiv \; b \cdot a_{*}^{-1} \bmod q\)
즉, 모듈러 나눗셈(modulo division)은 모듈러 곱셈 (modulo multiplication)으로 정의된다.📍 중요한 차이점:
- 일반적인 나눗셈은 실수(real number)를 결과로 내지만,
모듈러 나눗셈은 항상 정수(integer)를 결과로 낸다.
(이는 $b$와 $a_{*}^{-1}$ 모두 정수이기 때문)
- 일반적인 나눗셈은 실수(real number)를 결과로 내지만,
- 마지막으로, 정수 $a$의 모듈러 역원은 확장 유클리드 알고리즘 (Extended Euclidean Algorithm)을 이용해 계산할 수 있다.
- 중심 잔여 표현 (Centered Residue Representation)
Canonical은 0부터 시작하는 잔여계, Centered는 0을 기준으로 대칭인 잔여계다
지금까지 잔여(나머지, Residue)를 양의 정수(positive integer)라고 가정했다.
모듈러 $q$에서 가능한 나머지 집합은 다음과 같다.
\({0, 1, 2, \dots q-1}\)→ 이 표현 방식을 표준 잔여계(canonical residue system) 또는 비부호형 잔여 표현 (unsigned residue representation) 이라고 부른다.
🔸 하지만 또 다른 표현 방식도 존재한다.
바로 부호형 잔여계 (signed or centered residue system) 로, 잔여들이 0을 중심으로 대칭되게 분포한다. \({-\frac{q}{2}, -frac{q}{2}+1, \dots, 0, \dots, frac{q}{2}-2, \frac{q}{2}-1}\)→ 비부호형 잔여계나 부호형 잔여계 모두 잔여의 개수는 동일하게 $q$개이다. 차이는 단지 잔여 범위의 기준점(upper/lower bound)에 있다.
표현 방식 잔여 집합 하한(lower bound) 상한(upper bound) Canonical (Unsigned) $\{0, 1, 2, \dots, q-1\}$ 0 $q-1$ Centered (Signed) $\{-\frac{q}{2}, \dots, 0, \dots, \frac{q}{2}-1\}$ $-\frac{q}{2}$ $\frac{q}{2}-1$ 💡 모듈러 연산의 역할
모듈러 연산은 주어진 값을 위 두 시스템 중 하나의 잔여 범위로 변환한다.- 값이 상한보다 크면 → 모듈러스 $q$를 빼준다
- 값이 하한보다 작으면 → 모듈러스 $q$를 더해준다
→ 따라서 두 시스템의 차이는 단지 잔여의 “표현 방식”일 뿐, 모두 동일한 모듈러 집합 $\mathbb{Z}_q$를 나타낸다.
\[\mathbb{Z}_q = \{0, 1, 2, \dots, q - 1\}\]
Canonical과 Centered 잔여계는 모든 연산 성질이 동일하게 유지된다.
표준 잔여계(canonical system)와 중심 잔여계(centered system)는 덧셈 $\cdot$ 뺄셈 $\cdot$ 곱셈 $\cdot$ 나눗셈의 모든 모듈러 성질은 동일하게 성립한다.
\[(a \pm b) \bmod q, \quad (a \times b) \bmod q, \quad (a \div b) \bmod q\]→ 이들이 어떤 잔여계에서 계산되든 결과의 동치 관계는 변하지 않는다.
💡 이유:
두 시스템 모두 같은 모듈러스 $q$를 사용하기 때문에,
어떤 두 동치 잔여(congruent residues)라도 서로 $kq$의 차이를 가진다.
즉,
\(a \equiv b \pmod q \quad \Rightarrow \quad a - b = kq \quad (k \in \mathbb{Z})\)→ 따라서 canonical 표현이든 centered 표현이든, 각 연산의 결과는 항상 같은 동치류(congruence class)에 속하게 된다.
Canonical과 Centered 잔여계의 연산 성질 중 역원도 동일하게 유지된다.
모듈러 $q$에서 $a$의 역원은 다음을 만족한다.
\[a \cdot a^{-1} \equiv 1 \pmod q\]🔹 부호형(signed) 잔여 표현을 사용하는 이유는 특정 상황에서 모듈러 연산을 생략할 수 있을 정도로 계산을 단순화할 수 있기 때문이다.
#### 🧩 예제 1. Canonical (Unsigned) Representation 표준 잔여계에서는
\[(a + b) \bmod q = a + b\]
\((a + b) \bmod q\) 의 형태를 가정하자.
만약 어떤 애플리케이션에서 항상 $0 \le a + b \le q - 1$ 이라는 조건이 보장된다면,따라서 모듈러 연산을 생략할 수 있다.
(즉, 값이 잔여 범위 $[0, q-1]$를 벗어나지 않기 때문)#### 🧩 예제 2. Centered (Signed) Representation 이번에는 중심 잔여계에서
\[(a - b) \bmod q = a - b\]
\((a - b) \bmod q\) 를 생각하자.
만약 $a - b$가 항상 $[-\frac{q}{2}, \frac{q}{2} - 1]$ 범위 안에 있다면,이때도 모듈러 연산을 생략할 수 있다.
#### ⚠️ 주의: Canonical 표현에서의 뺄셈 만약 위와 같은 $(a - b) \bmod q$ 연산을 canonical 표현으로 계산한다면,
$a - b$가 음수일 경우 그 값은 하한(0)보다 작아진다.
이 경우 모듈러스 $q$를 하나 이상 더해주는(modulo reduction) 보정이 필요하다.예를 들어,
\(a = 3, \quad b = 7, \quad q = 11\)
이면
\((a - b) \bmod 11 = (3 - 7) \bmod 11 = (-4) \bmod 11 = 7\)✅ 정리:
- canonical 표현: 음수가 되면 반드시 모듈러 보정 필요
- centered 표현: ±범위 안이면 모듈러 보정 없이 연산 가능
즉, 부호형(centered) 잔여 표현은 덧셈보다 뺄셈 연산에서 더 직관적이며 효율적이다.
§D-5.8 절에서는 centered residue representation의 유리한 성질을 활용하여 FastBConvEx 연산(Fast Balanced Convolution Extension) 을 설계한다.
- 이 알고리즘에서는 다음과 같은 관계가 성립한다.
일반적으로는 모듈러 연산이 필요하지만,
\[-\frac{b^{\alpha}}{2} \leq \mu + u < \frac{b^{\alpha}}{2}\]
이때 $\mu + u$가 항상 centered residue 범위 내에 존재함이 보장된다.따라서, \((\mu + u) \bmod b^{\alpha} = \mu + u\)
즉, 모듈러 연산을 생략하고 단순 덧셈으로 표현할 수 있다.
이는 연산을 간소화하고 계산 효율을 높이는 핵심 아이디어이다.💡 핵심 포인트:
- centered residue 표현을 사용하면,
값이 잔여 범위를 벗어나지 않는 한 모듈러 처리가 불필요하다. - 이 특성은 고속 암호 연산(예: FastBConvEx) 설계 시
불필요한 나머지 계산을 제거하여 성능을 최적화하는 데 사용된다.
</div>
</details>
Introduction to Homomorphic Encryption
Published: Updated:
해당 포스트는 서울대학교 천정희 교수님의 암호론 강의를 기반으로 작성하였다. 이번 포스트에서는 ‘동형암호의 개요’에 대한 내용을 요약•정리하고자 한다.
동형암호의 개요
1) 동형암호란?
📘 4세대 암호
- 암호화된 상태에서 계산이 가능한 암호로, 키를 갖고 있지 않아도 계산이 가능하다.
→ 키를 보호하는 암호로, 키가 덜 사용된다는 측면에서 키의 안전성이 높은 암호이다.
- 미래 컴퓨팅 환경: 완벽한 하인!
- 우리가 하려는 일의 비밀을 알지 못한 채, 빠르고 정확하게 대신 수행하는 컴퓨터
📘 사례 모음집
- 사례 1: 개인 클라우드 - 데이터를 맡기되, 비밀은 지키기 (대칭키 동형암호)
- 스토리지 클라우드: Dropbox, Google email/calendar, NAS
- 사용자는 데이터를 암호화하여 저장하지만, 클라우드는 복호화 키를 모름
→ 그래도 사용자는 평문처럼 검색하거나 접근 가능함 - 단순한 대칭키 암호는 서버가 데이터를 전혀 활용할 수 없지만, 대칭키 동형암호를 사용하면 암호문 상태에서도 검색·분석이 가능
→ 예: 스팸 필터링, 파일 이름 검색 등
- 사용자는 데이터를 암호화하여 저장하지만, 클라우드는 복호화 키를 모름
- 계산 클라우드: DNA 계산, 헬스케어, 개인성향분석을 통한 추천
- 개인의 민감한 데이터를 암호화한 채 클라우드에 맡겨 계산 가능
- 복호화 키는 오직 데이터 소유자가 보유
→ 이러한 형태의 계산을 대칭키 동형암호라고 함
- 스토리지 클라우드: Dropbox, Google email/calendar, NAS
- 사례 2: 다수 사용자 통계분석 - 데이터를 공유하되, 통제는 유지하기
- 개인정보기반 마케팅 (구글, 페이스북, 네이버 등)
- 사용자의 데이터가 허용된 범위 내에서만 활용되도록 제한 가능
→ 예: 내가 ‘광고에 사용’ 옵션을 허용한 경우에만 마케팅 분석 수행 - 동형암호를 통해 ‘데이터는 사용하되, 직접 보지는 못하게’ 할 수 있음*
- 사용자의 데이터가 허용된 범위 내에서만 활용되도록 제한 가능
- 정부 데이터베이스: 교육, 의료, 납세
- 기관 간 민감 데이터 교류시, 동형암호 기반 연산으로 프라이버시 보장 가능
- 개인정보기반 마케팅 (구글, 페이스북, 네이버 등)
- 동형암호 (Homomorphic Encryption, HE)
- 복호화 없이도 연산이 가능한 암호화 기술, 즉 데이터를 보지 않고도 계산할 수 있는 암호
📘 참고. 영지식 증명 (Zero-Knowledge Proof, ZKP)
- 2017년, 영지식 (Zero-Knowledge) SNARG 계산 증명 기술 등장
- 연산 결과를 직접 공개하지 않고도 “올바르게 계산되었음”을 증명할 수 있음
- 즉, 비밀은 보호하면서도 신뢰를 확보하는 기술
→ 대표 활용: 블록체인 개인정보 보호, 신원 인증, 거래 검증
📘 동형암호의 작동 원리
예를 들어, 우리가 1 + 2라는 단순한 계산을 하고 싶다고 하자. 하지만 계산의 내용을 클라우드에 노출하고 싶지 않다. 이때 우리는 각 값을 암호화하여 클라우드에 보낸다. 예를 들어, 1은 33, 2는 54로 암호화된다.
클라우드는 복호화 키를 전혀 알지 못한 채 단순히 암호문끼리의 덧셈(33 + 54)을 수행한다. 계산 결과로 얻은 87은 여전히 암호화된 상태이며, 우리는 이 값을 받아서 복호화하면 최종적으로 3을 얻는다.
이처럼 동형암호는 단순한 산술 연산뿐만 아니라 영상 처리나 머신러닝 모델 추론과 같은 복잡한 계산에도 확장될 수 있다. 예를 들어, 클라우드에게 두 장의 이미지를 암호화된 상태로 보내 “이 두 이미지가 같은지 비교해 달라”고 요청할 수 있다. 클라우드는 이미지 내용을 직접 보지 않고도 연산을 수행해 결과값만을 사용자에게 반환할 수 있다.

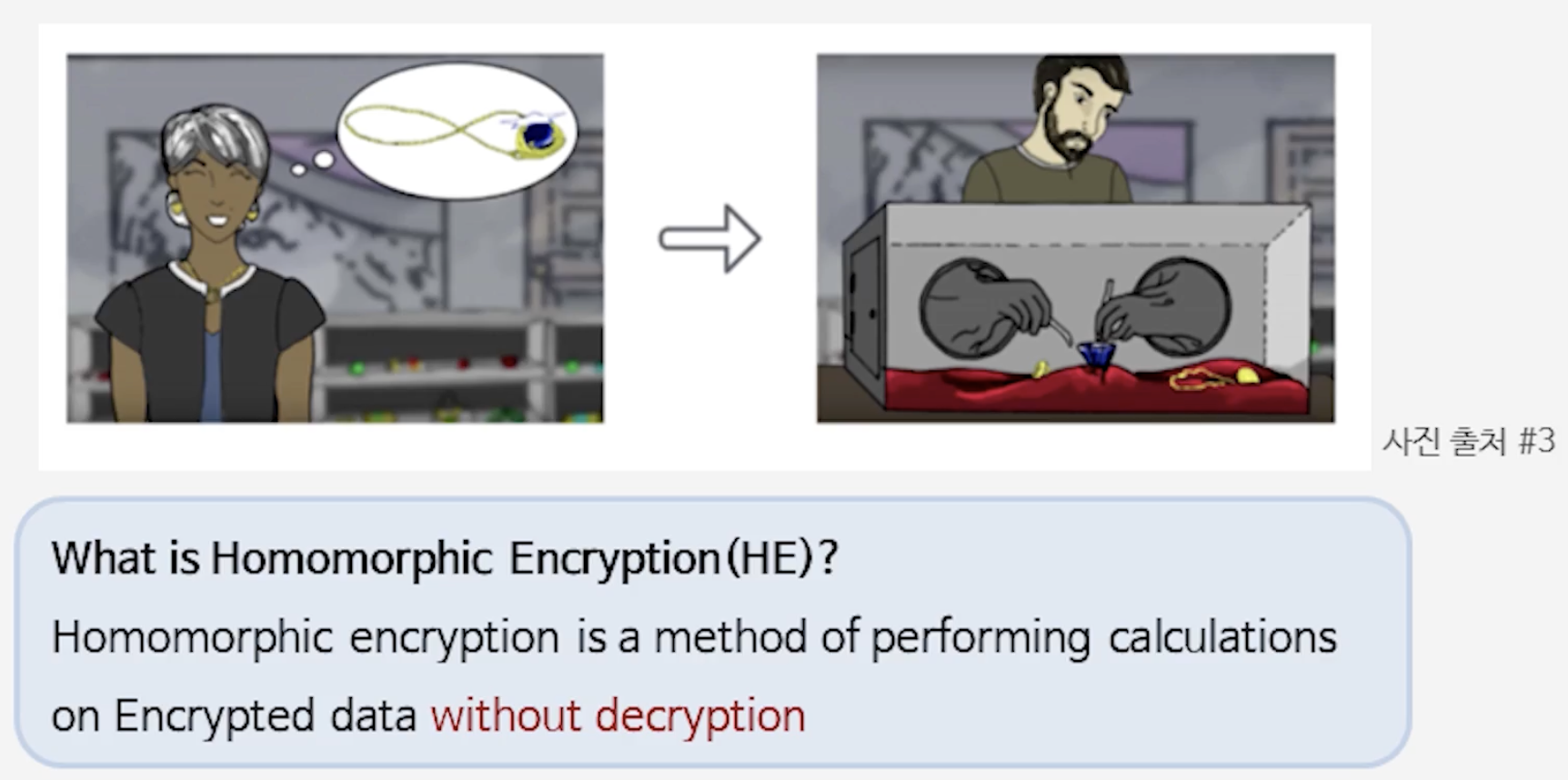
📘 동형암호의 직관적 설명
간단한 비유로 설명하면, 전통적인 암호는 열쇠가 있어야만 여는 금고와 같습니다. 키가 없으면 그 안에 무엇이 있는지 전혀 알 수 없고, 아무런 조작도 할 수 없습니다.
반면 동형암호는 “말랑말랑한 금고”와 비슷합니다. 금고 안의 내용(평문)은 외부에서 보이지 않지만, 외부에서 손(연산)을 넣어 내부의 값을 가공할 수 있습니다. 즉, 클라우드(연산자)는 복호화 키를 알지 못한 채도 암호문 위에서 덧셈·곱셈 같은 연산을 수행할 수 있고, 최종 결과는 여전히 암호화된 상태로 반환됩니다. 사용자는 그 결과를 복호화해 실제 정답을 얻습니다.
예시: 의료 데이터의 경우, 환자의 원본 기록은 열리지 않은 상태로 보관됩니다. 연구자는 이 암호화된 데이터를 클라우드에 맡겨 통계분석이나 모델 추론을 수행하게 하고, 클라우드는 내용을 보지 못한 채 계산만 수행합니다. 계산 결과(예: 위험 지표)는 암호화된 상태로 돌아오고, 복호화 권한이 있는 사람만이 필요한 정보(예: 특정 진단의 유무 또는 요약된 수치)만 확인합니다.
핵심은 "비밀은 지키면서도 필요한 계산은 수행할 수 있다"는 점입니다. 이 성질 덕분에 동형암호는 개인정보·의료·금융 데이터의 안전한 외부 계산(클라우드 기반 분석, 암호화된 ML 추론 등)에 유용합니다.
- 동형암호의 장·단점
- 장점: 튜링완전성 (Turing-Complete)
- 암호화된 상태에서 AND, OR, NOT 연산이 모두 가능하다. 즉, 컴퓨터가 수행할 수 있는 모든 연산 (검색·통계처리·머신러닝)을 암호화된 데이터 위에서 수행할 수 있다.
→ 따라서 데이터 유출 위험을 원천 차단할 수 있다.
- 암호화된 상태에서 AND, OR, NOT 연산이 모두 가능하다. 즉, 컴퓨터가 수행할 수 있는 모든 연산 (검색·통계처리·머신러닝)을 암호화된 데이터 위에서 수행할 수 있다.
- 단점
- 암호문 크기 확장: 평문 대비 약 $10$ ~ $100K$배 (대칭키 방식은 약 $0.1$ ~ $1K$ 배 수준)
- 암·복호화 속도 저하: AES ≈ $1 us$, RSA ≈ $1 ms$, HE ≈ 수십 $ms$
- 암호문 연산 속도 저하: 특히 곱셈 연산은 평문 계산 대비 수백 배 이상 느림
- 응용별 성능 편차: 연산의 종류 (덧셈·곱셈·비교)에 따라 속도 차이가 크며, 효율을 높이기 위해 개별 최적화 알고리즘 및 구현 기술이 필요함
📘 예시 (복잡도 관점의 단순 모델)
- 128-bit 보안을 만족하기 위해 키 크기를 50배 늘린다고 가정하면, 계산량은 일반적으로
O(n^2)복잡도를 가지므로 $50^2x = 2,500x$ 배 증가하게 된다.- 그러나 빠른 곱셈 알고리즘 (Fast Multiplication)을 적용하면 복잡도는
O(nlog n)수준으로 개선되어 $(50 \log 50)x ≈ 2,000x$ 정도로 줄어든다.👉 따라서, 키 길이를 $50$배 늘려도 계산량은 약 $2,000$배 증가하게 된다. 즉, 보안 강도를 높이는 것은 필연적으로 연산 비용 증가를 수반한다.
- 물론 위 계산은 최적화가 잘 이루어진 경우를 가정한 것이다. 실제로는 알고리즘과 구현 수준에 따라 성능 편차가 크며, 이러한 최적화(optimization)는 인공지능이 아니라 사람이 직접 설계해야 한다. 다시 말해, 알고리즘적·구현적 튜닝이 부족한 경우에는 여전히 수천 배에서 수만 배까지 느린 사례도 존재한다.
- 장점: 튜링완전성 (Turing-Complete)
2) 동형암호의 종류
- 정수 기반 동형암호 (Integer-based HE scheme)
동형암호의 초기 형태는 **정수 연산 기반**으로 설계되었습니다. 대표적으로 RAD PH와 DGHV 스킴이 있습니다.
- RAD PH Scheme
- 키 생성
- Secret Key: large prime $p$
- Public Key: $n = p q_0$
- 암호화 (Encryption) : $Enc(m) = m + p q \pmod{n}$
- 복호화 (Decryption) : $Enc(m) \bmod p = m$
덧셈 연산
\(Enc(m_1) + Enc(m_2) = (m_1 + p q_1) + (m_2 + p q_2) = (m_1 + m_2) + p(q_1 + q_2) = Enc(m_1 + m_2)\)- ✅ 결과:
평문 덧셈이 암호문 덧셈으로 보존되므로 부분동형(ADD-homomorphic) 속성을 가진다.
그러나 INSECURE — 잡음(noise) 누적과 키 복원 공격에 취약하다.
- 키 생성
- DGHV HE scheme (on $\mathbb{Z}_{2}$)
- 암호화 : $Enc(m) = m + 2e + p q$
- $m \in {0,1}$: 메시지 비트
- $e$: 작은 노이즈 (error term)
- $p, q$: 큰 정수
- 특징
- 양자 컴퓨팅에 대해 안전 (Post-Quantum Secure)
- 정수 기반 대신 다항식 링 구조를 사용하는 고도화된 확장 버전 존재:
$R_q = \mathbb{Z}_q[x] / (x^n + 1)$
- ✅ 의의:
DGHV는 Craig Gentry의 Fully Homomorphic Encryption (FHE)의
초기 형태로, “잡음을 제어하며 연산을 확장하는” 아이디어의 기반이 되었다.
- 암호화 : $Enc(m) = m + 2e + p q$
</div>
- RAD PH Scheme
</details>
Post-Quantum Cryptography
Published: Updated:
해당 포스트는 서울대학교 천정희 교수님의 암호론 강의를 기반으로 작성하였다. 이번 포스트에서는 ‘양자내성암호’에 대한 내용을 요약•정리하고자 한다.
1. 양자내성(Quantum-resistant) 공개키암호
1) 양자 컴퓨터의 전망
- 약 15년 이내에 기존 암호를 공격할 수준의 양자 컴퓨터 도래 예상
📘 양자컴퓨터, 정말 만들 수 있을까?
양자컴퓨터, 아직은 Open Problem
- 양자컴퓨터를 충분히 큰 규모로 만들 수 있느냐는 아직도 open problem이다.
- 현재 우리는 소규모의 양자 비트(Qubit)를 다루는 장치는 만들었지만, 이를 scalable하게 확장할 수 있을지는 불확실하다.
- 양자컴퓨터는 0과 1을 동시에 다루지만, 이로 인해 잡음(noise)와 decoherence가 심각해지고, 여러 큐비트를 동시에 안정적으로 제어하는 것이 매우 어렵다.
- 그래서, 예를 들어 1,000큐비트로 확장하게 되면 오류(Error)가 너무 커진다.
양자컴퓨터의 두 가지 구현 방식
- Quantum Gate 방식: 전통적으로 암호학에 위협적인 방식이지만, 현재 발전 속도는 더딘 편이다.
- Quantum Annealing(어닐링) 방식: D-Wave, Google 등에서 이미 수백 큐비트까지 구현했으나, 이 방식은 암호를 다항식 시간 내에 깨지는 못한다.
대신, 검색·최적화 문제를 빠르게 푸는 데 유용하며, 실제로 산업 응용에서 활발히 연구 중이다. - 따라서, 암호를 직접적으로 해독할 수 있는 게이트 기반 양자컴퓨터가 언제 등장할지는 불확실하다.
어떤 전문가는 15년, 또 어떤 전문가는 150년을 예상할 정도로 의견 차이가 크다.
- 현재 널리 쓰이는 모든 공개키 암호(ECC/RSA 등)은 Shor’s Algorithm 때문에 공격 가능
📘 Shor's Algorithm 자세히 보기
- Shor의 알고리즘은 인수분해와 이산로그 문제의 복잡도를 지수적(exponential)에서 다항식(polynomial) 수준으로 낮춘다.
- 따라서 현재 우리가 사용하는 RSA, ECC 같은 공개키 암호는 양자컴퓨터에서 효율적으로 깨질 수 있다.
- 예: 약 1,000 큐비트 정도의 양자컴퓨터가 현실화되면 RSA-2048 수준의 암호도 짧은 시간 안에 풀릴 수 있다고 예측한다.
- 반면, 대칭키 암호/해쉬 함수는 키의 길이, 해쉬의 길이를 두 배로 늘리면 기존 수준의 보안성 유지 가능
2) Contemporary Cryptography
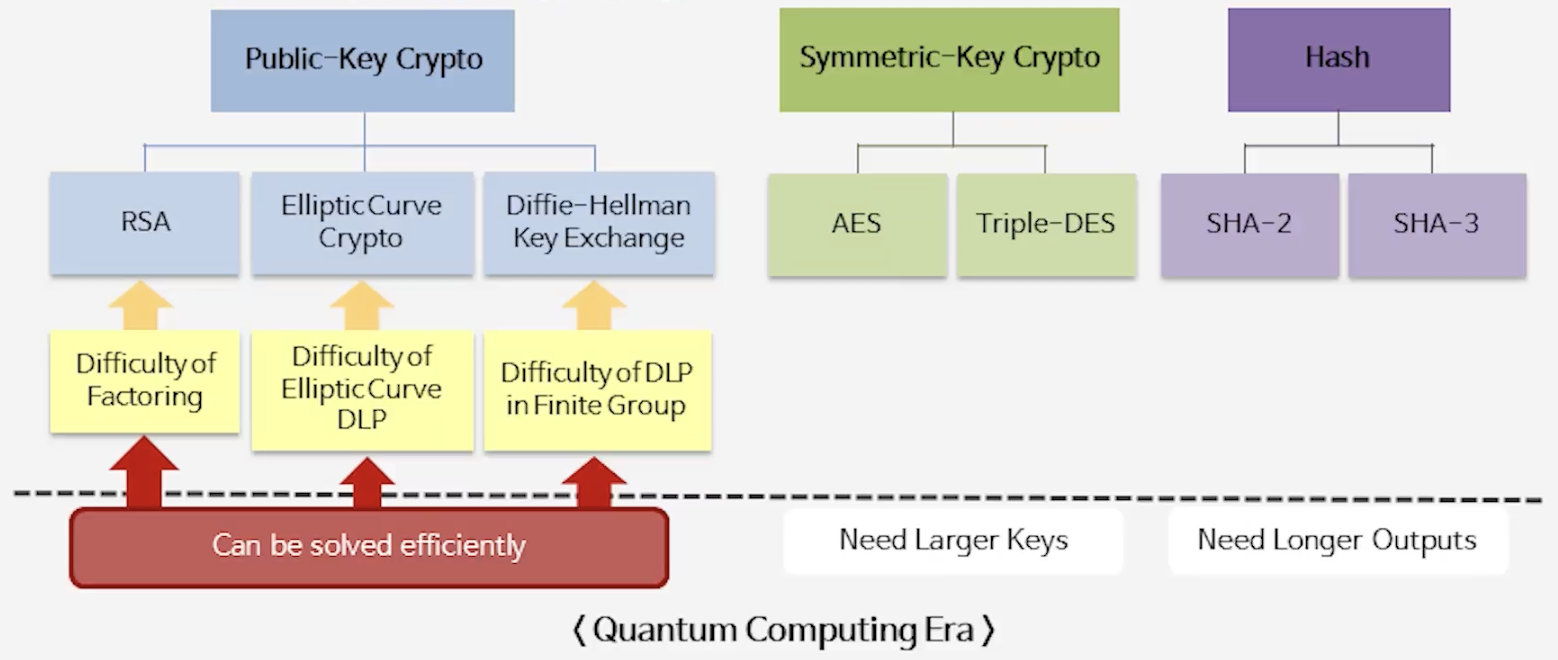
- 공개키 암호 (RSA, ECC, DH): Shor 알고리즘 때문에 안전하지 않음 → 비트 수 늘려도 소용 없음
- 대칭키 암호 (AES 등): 키 길이를 2배로 늘리면 안전성 유지 가능 (예: AES-256 권장)
해시 함수 (SHA 계열): 출력 길이를 3배로 늘려야 같은 수준의 보안성 유지 가능
- 요약: 누가 무엇에 영향주는가
- Shor’s algorithm: 공개키 암호(인수분해·이산로그 기반)를 양자환경에서 다항식 시간(polynomial time) 내에 풀어버리는 알고리즘 → 공개키 계열은 근본적 위협
- Grover’s algorithm: 대칭키/해시의 무차별 공격을 제곱근(quadratic) 속도로 가속화하는 알고리즘 → 완전 붕괴는 아니며, 키/출력 길이를 늘려 방어 가능
📘 왜 이렇게 되는 걸까?
- 공개키 (Shor)
- 고전적 최선: 인수분해·이산로그는 지수 시간(대략 $(2^{n})$ 또는 유사) 소모
- Shor: 이를 다항식 시간(예: poly($n$))으로 해결 → 비트 길이 확대만으로는 방어 불가
- 대칭키 (Grover)
- 고전적 무차별 검색: $O(2^{n})$ (키 길이: $n$)
- Grover: $O(2^{\frac{n}{2}})$으로 가속 — 즉 제곱근(Quadratic) 속도 향상
- 결과: 키 길이를 2배 하면 기존 수준의 보안 유지 가능 (예: AES-128 → AES-256 권장)
- 해시(충돌/프리이미지)
- 고전적 충돌 저항: $2^{\frac{n}{2}}$ (출력 길이: $n$)
- 양자 영향 하의 충돌/프리이미지 복잡도는 알고리즘과 공격 모델에 따라 달라지지만, 실무에서는 출력 길이를 충분히 늘림(권장: 약 3배 규칙)으로 안전성을 확보하는 관점이 사용
- 따라서 “128비트 수준의 안전성”을 목표로 하면 출력 길이를 256비트가 아니라 더 늘려(약 384비트 권장)야 한다는 주장으로 정리되는 경우가 있음
3) Post-Quantum Cryptography (1)
- 2016년, 미국 국가안보국(NSA)은 “머지않은 미래(not too distant future)에 Post-Quantum Cryptography (PQC)로 전환하겠다”고 발표
- 곧바로 미국 국립표준기술연구소(NIST)가 PQC 표준화 프로젝트를 시작하면서 오늘날의 Kyber, Dilithium 등 PQC 알고리즘 경쟁이 본격화
- 목표: Post-Quantum 공개키 암호(Encryption / Signature / Key Exchange)의 표준화
📘 당시 상황을 조금 더 살펴보기
- 당시 미국 정부는 Suite A/B 암호 체계를 따랐는데, Suite B에는 AES와 ECC를 포함한다
- 즉, 미국과 외국 정부가 안전하게 통신하려면 ECC 지원이 필수였다.
- 그런데 NSA가 ECC 도입을 중단하고 PQC로 전환하겠다고 선언하면서, 사실상 전 세계가 따라야 하는 신호가 되었다.
- NSA 발표 직후, NIST는 2016년 가을 Call for Proposals, 2017년 Submission 마감 일정을 공개하며 PQC 표준화 작업에 착수했다.
4) Post-Quantum Cryptography (2)
- 양자내성암호의 전제 조건
- 가설 1. $P ≠ NP$
→ 양자컴퓨터가 등장해도 $NP$ 문제 전체를 쉽게 풀 수 있다는 근거는 없다. - 가설 2. NP-hard 기반 안전성
→ 암호는 보통 NP-hard 문제와 동치가 아니라, 그 위에 기반한다고 본다.
📘 더 자세히 보기
- 가설 1 (P ≠ NP)
- 퀀텀 알고리즘은 병렬화와 유사한 성질을 보이지만, NP 문제 전체를 풀 수 있다는 증거는 없다.
- 따라서 P와 NP의 분리는 유지된다고 보는 것이 일반적이다.
- 가설 2 (기반 vs. 동치)
- 암호 설계에서 특정 NP-hard 문제와 정확히 동치임을 보장할 수는 없다.
- 하지만 “그 문제를 기반으로 한다(based on)” 정도면 연구자 사회에서 충분히 인정한다.
- 예: RSA는 인수분해와 동치는 아니지만, 인수분해 문제에 기반해 안전성을 설명한다.
- 가설 1. $P ≠ NP$

- Lattice-based가 주목받는 이유
- 보안성: 난이도가 높은 격자 문제(lattice problems) 에 기반 (NP-hard)
- 효율성: 구현이 빠르고, 실제 하드웨어/소프트웨어에 적합
- 범용성: 동형암호(HE), 신원기반암호(IBE) 등 다양한 응용 가능
- 동형암호(HE): 암호화된 상태에서 연산을 직접 수행할 수 있는 암호
- 신원기반암호(IBE): 이메일 주소 같은 신원 자체를 공개키로 삼는 암호
5) 경량 (Light Weight) 공개키암호
- 기존 공개키 암호의 기반 난제: 지수승 연산 (예. RSA, ECC → $a \mapsto a^b$)
- 지수 연산은 본질적으로 계산량이 크고, 효율성에도 한계가 있음
- 그렇다면, “지수승 대신 곱셈만으로도 안전한 암호를 만들 수 없을까?”란 질문이 나옴
- 곱셈은 지수승보다 계산이 훨씬 빠르지만 (제곱 정도의 계산량),
$a \mapsto ab$는 너무 단순해서 일방향 함수로 쓰기에는 안전성 부족
- 곱셈은 지수승보다 계산이 훨씬 빠르지만 (제곱 정도의 계산량),
📘 Lattice 접근법
- 격자 기반 암호는 단순 곱셈 $ab$에 노이즈(잡음)를 더해서 문제를 어렵게 만든다.
- $a \mapsto ab + \text{noise}$ 형태
- 계산량은 quadratic 수준을 유지하면서도, 노이즈 때문에 문제는 어렵게 정의된다.
- 노이즈가 들어가면 단일 해답이 아니라 많은 경우의 수(case)가 생겨서 공격이 어렵다.
→ 이런 성질 덕분에 Lattice 기반 암호는 효율성(빠름)과 안전성(어려움) 을 동시에 노릴 수 있다.
2. 격자기반 양자내성암호
1) Geometry of Numbers: Lattices (1)
- 격자란 무엇인가?
- 격자(Lattice)는 $\mathbb{R}^n$ 안에 있는 이산적인(discrete) 점들의 집합
- 이산적이란? 임의의 격자점에서 작은 원을 그리면, 그 안에는 자기 자신만 있고 다른 격자점은 들어오지 않는다.
- 일차독립 벡터 $v_1, \dots, v_m \in \mathbb{R}^n$이 주어지면, \(L = \mathbb{Z}v_1 + \cdots + \mathbb{Z}v_m\) (선형결합)로 정의
📘 기저 (Basis)와 기저 행렬
- 기저 (Basis)
- $v_1, \dots, v_m$을 격자의 기저(basis)라고 한다.
- 이 기저 벡터들을 정수배해서 나오는 모든 점들이 격자점이다.
- 벡터공간의 기저와 비슷하지만, 차이가 있다 → 벡터공간은 실수배/유리수배를 허용하지만, 격자는 정수배만 허용한다.
- 기저 행렬 (Basis Matrix)
- 기저 벡터들을 모아 $B = [v_1 ; v_2 ; \cdots ; v_m]$라고 하면,
모든 격자점 $v$는 \(v = Bx, \quad x \in \mathbb{Z}^m\) 형태로 쓸 수 있다.
- 기저 벡터들을 모아 $B = [v_1 ; v_2 ; \cdots ; v_m]$라고 하면,
📘 격자의 부피 (Determinant)
- 격자의 부피(Det(L))는 기저 벡터들이 만드는 평행다면체(parallelepiped)의 부피와 같다.
- \(\det(L) = \det[v_1 ; v_2 ; \cdots ; v_m]\) 로 정의된다.
- 💡 직관적으로, 2차원 (평행사변형의 넓이), 3차원 (평행육면체의 부피), 4차원 이상 (일반화된 평행다면체의 부피)
- 단, 정사각행렬이 아닐때는?
- 예: 3차원 공간에 벡터가 두 개만 있으면 3×2 행렬 → 정사각형 아님
- 이 경우, 두 벡터가 span하는 2차원 평면 위에서 생각한다.
- 즉, 그 평면 안에서 2×2 행렬로 다시 보고, 그 평행사변형의 넓이로 정의할 수 있다.
📘 정수론과 격자의 연결
- 정수론에는 원래 거리 개념이 없다.
→ 예: 모듈러 $p$에서 2와 5 중 어느 쪽이 더 크다고 말할 수 없다. - 하지만 격자를 도입하면 거리 개념을 가져올 수 있고, 덕분에 “가장 작은 해(솔루션)” 같은 문제를 논할 수 있다.
- 응용 예시: Four Square Theorem
→ 모든 자연수는 네 제곱수의 합으로 쓸 수 있다
\(n = a^2 + b^2 + c^2 + d^2\)
- 응용 예시: Four Square Theorem
- 격자(Lattice)는 $\mathbb{R}^n$ 안에 있는 이산적인(discrete) 점들의 집합
- 격자와 벡터공간의 차이
- 벡터공간에서는 실수( $\mathbb{R}$ )나 유리수( $\mathbb{Q}$ ) 배수가 허용
→ 예: 벡터를 $0.1$배, $1.5$배 등으로도 만들 수 있음 - 격자에서는 정수($\mathbb{Z}$) 배수만 허용
→ 예: 벡터를 $1$배, $2$배, $-3$배 하는 식
$\therefore$ 격자는 벡터공간의 “부분집합”이지만, 모든 점이 격자점인 것은 아니다.
- 벡터공간에서는 실수( $\mathbb{R}$ )나 유리수( $\mathbb{Q}$ ) 배수가 허용
- 격자의 어려운 문제들
- Shortest Vector Problem (SVP): 0이 아닌 가장 짧은 벡터를 찾는 문제 (어렵다).
- Closest Vector Problem (CVP): 임의의 점이 주어졌을 때 가장 가까운 격자점을 찾는 문제 (역시 어렵다).
- 이 난제들이 바로 격자 기반 암호의 안전성을 뒷받침한다.
2) Geometry of Numbers: Lattices (2)
- Shortest Vector Problem (SVP):
격자 $L$이 주어졌을 때, 0이 아닌 벡터 중에서 가장 짧은 벡터를 찾으시오.
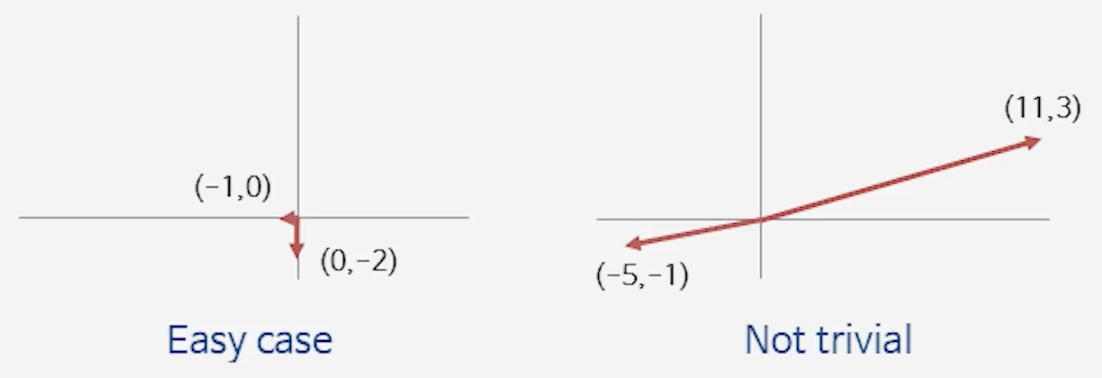
📘 어떤 경우에 어려울까?
- 직교 기저(orthogonal basis)일 때는 쉽다.
- 기저 벡터들이 서로 수직이라면, 임의의 점에서 정사영(projection)을 이용해 쉽게 가까운 격자점이나 최소 벡터를 찾을 수 있다.
- 예: (–1, 0)이나 (0, –2) 같은 경우 → 바로 확인 가능.
- 기저가 “누워 있는 경우(직교가 아닌 경우)”에는 어렵다.
- 기저 벡터들이 수직에서 멀어질수록, 한 점에 대해 가까운 후보 격자점이 여러 개 생긴다.
- 정사영 방식이 통하지 않아, 최소 벡터를 찾는 일이 훨씬 복잡해진다.
- 예: (–5, –1)과 (11, 3) 같은 벡터 → 어느 게 shortest인지 직관적으로 알기 어려움.
- 이 때문에 직교 기저가 중요하다.
실제로 격자 기저를 “직교에 가깝게” 바꿔주는 방법으로 Gram–Schmidt 정규화 같은 기법이 중요하게 쓰인다.
📘 기저를 좋게 만드는 과정
👉 Gram–Schmidt 정규화 (실수배 허용)
- 주어진 기저 벡터들을 서로 직교하는 기저로 바꿔주는 방법
- 벡터 $v_2$에서 $v_1$ 방향 성분을 빼주면, $v_1$과 직교하는 새로운 벡터가 된다.
- 이런 식으로 순차적으로 직교 성분을 제거하면, 원래와 같은 공간을 span하는 직교 기저를 얻을 수 있다.
단점: 격자는 정수배만 허용하는데, Gram–Schmidt는 실수배를 쓰므로 격자 안에서는 바로 적용 불가.
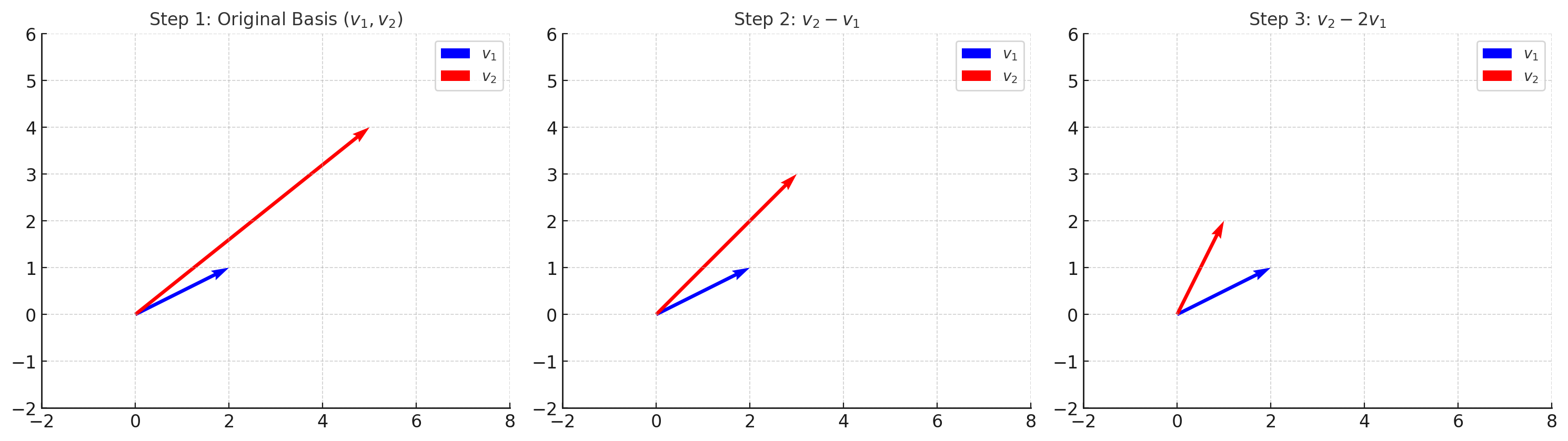
- Gram–Schmidt 정규화 (Step-by-Step)
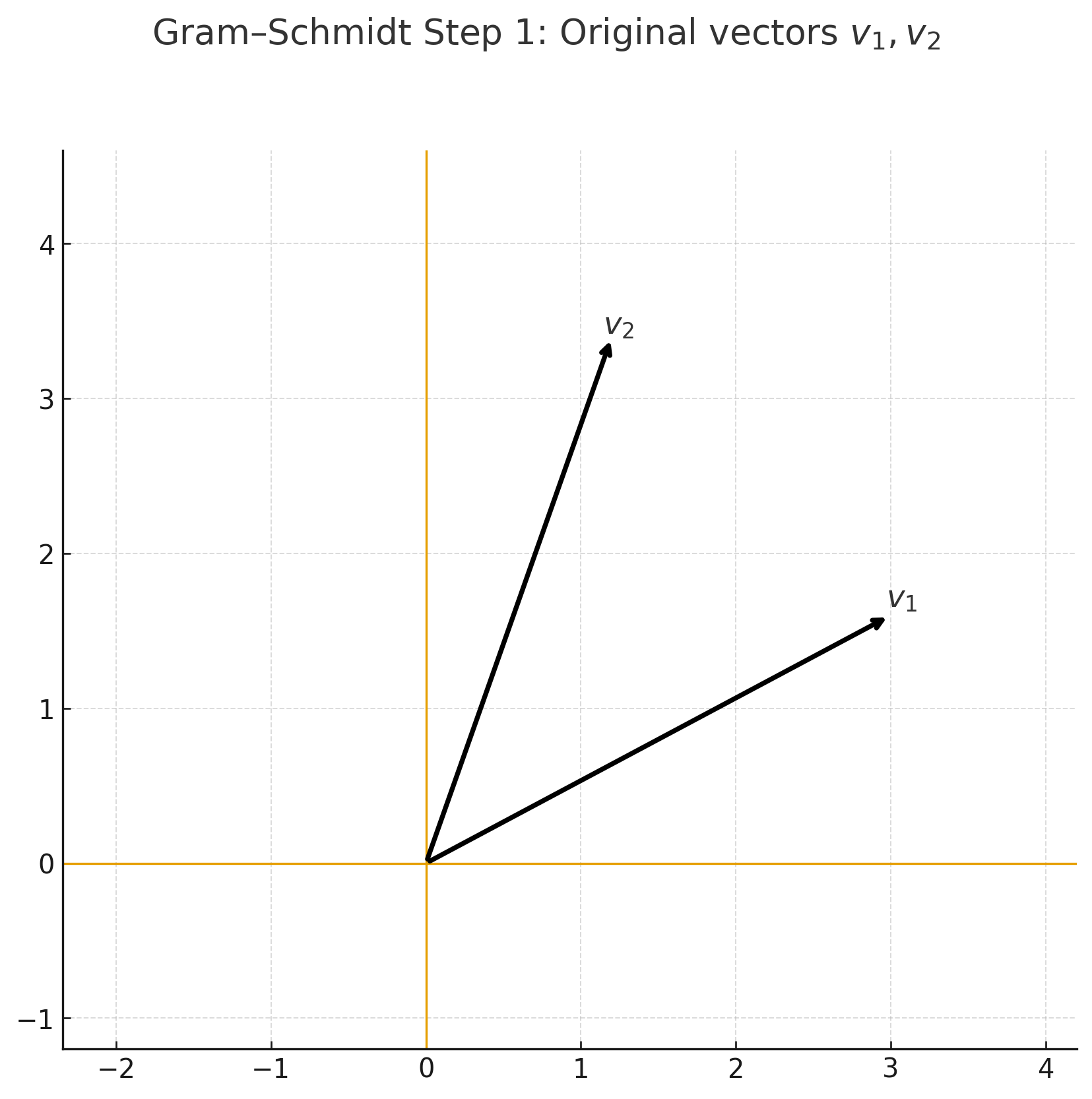 Step 1 — 원래 기저 \(v_1, v_2\) | 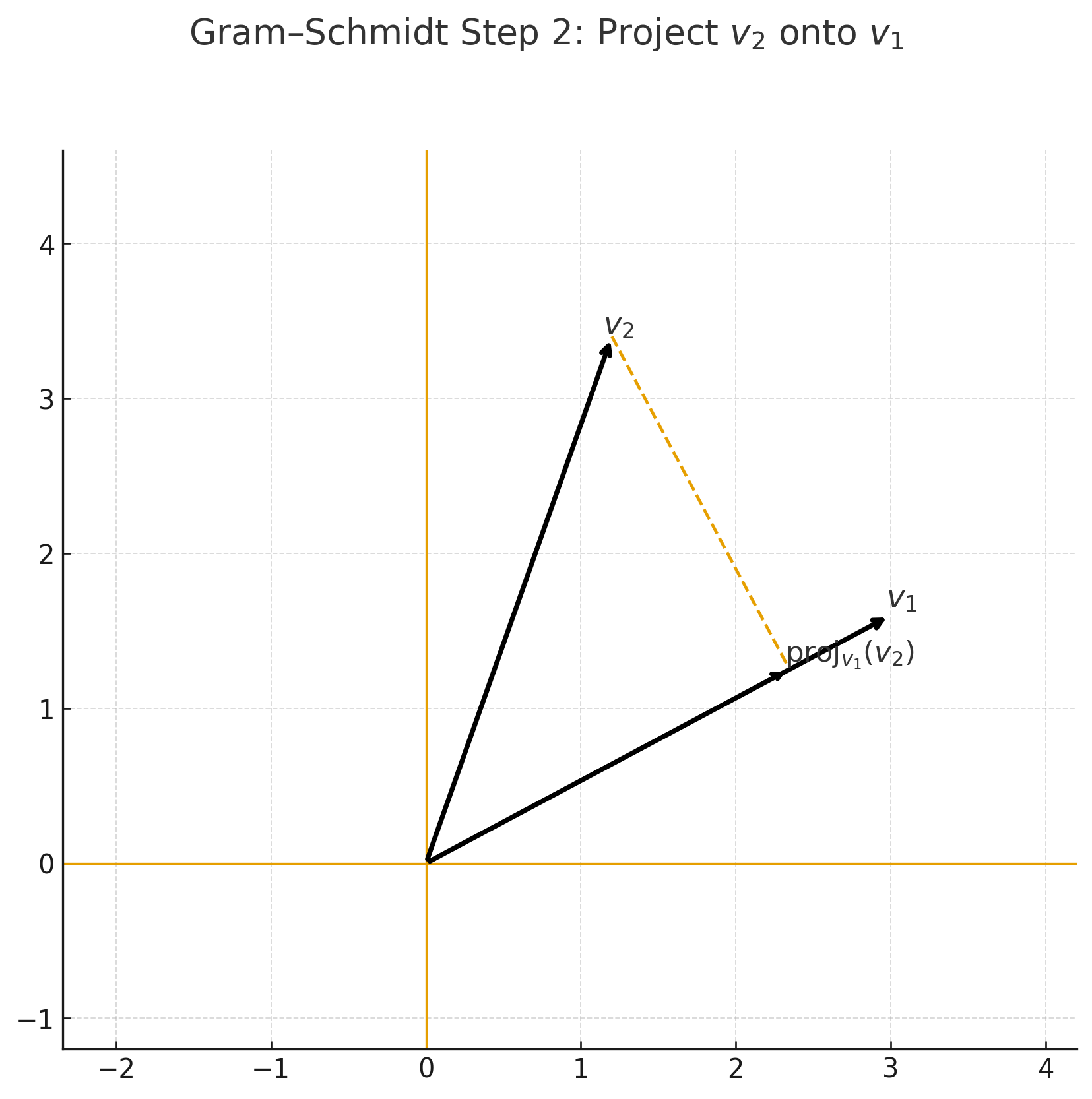 Step 2 — \(v_2\)를 \(v_1\) 위로 정사영 |
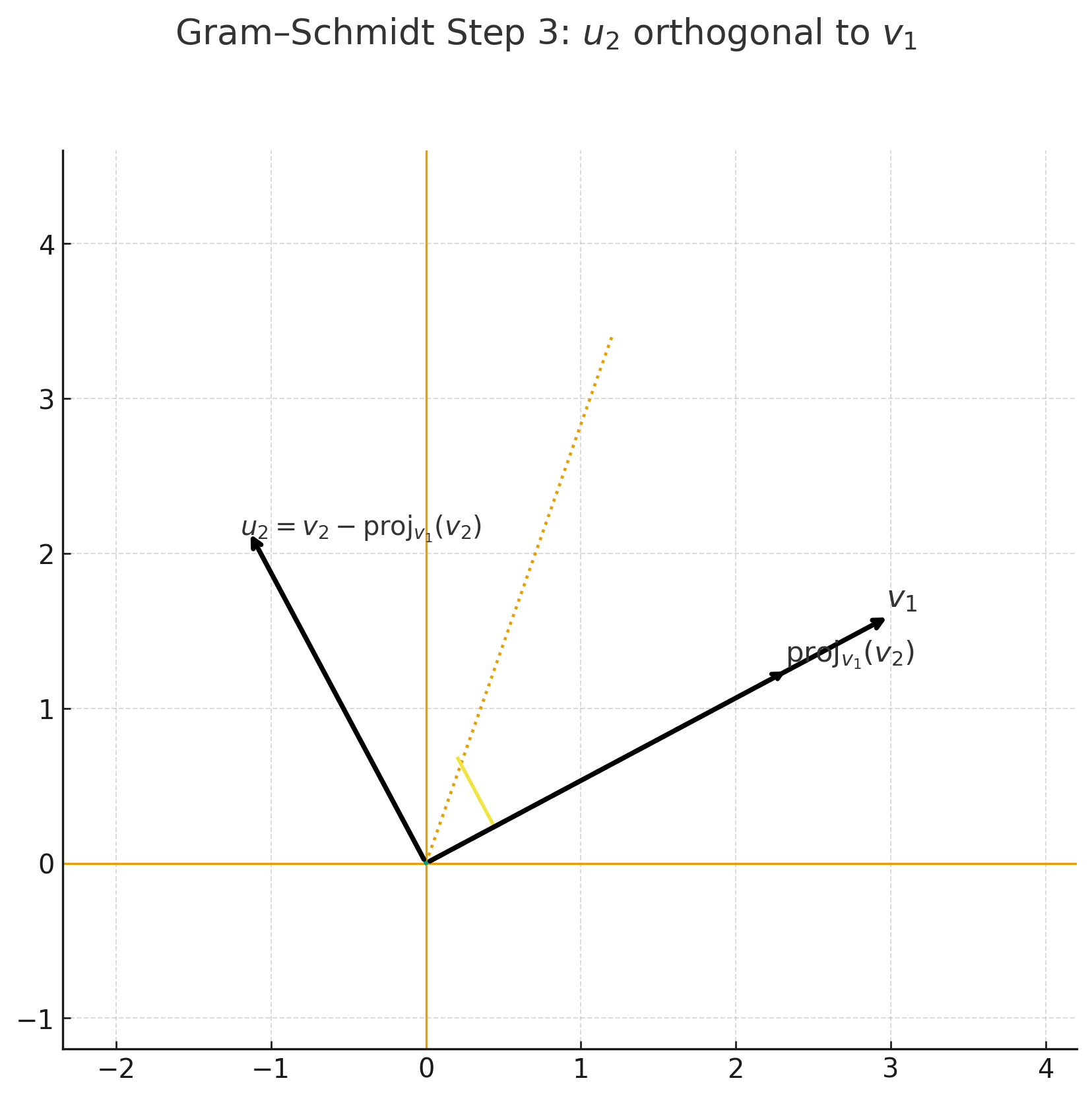 Step 3 — \(u_2 = v_2 - \mathrm{proj}_{v_1}(v_2)\) | 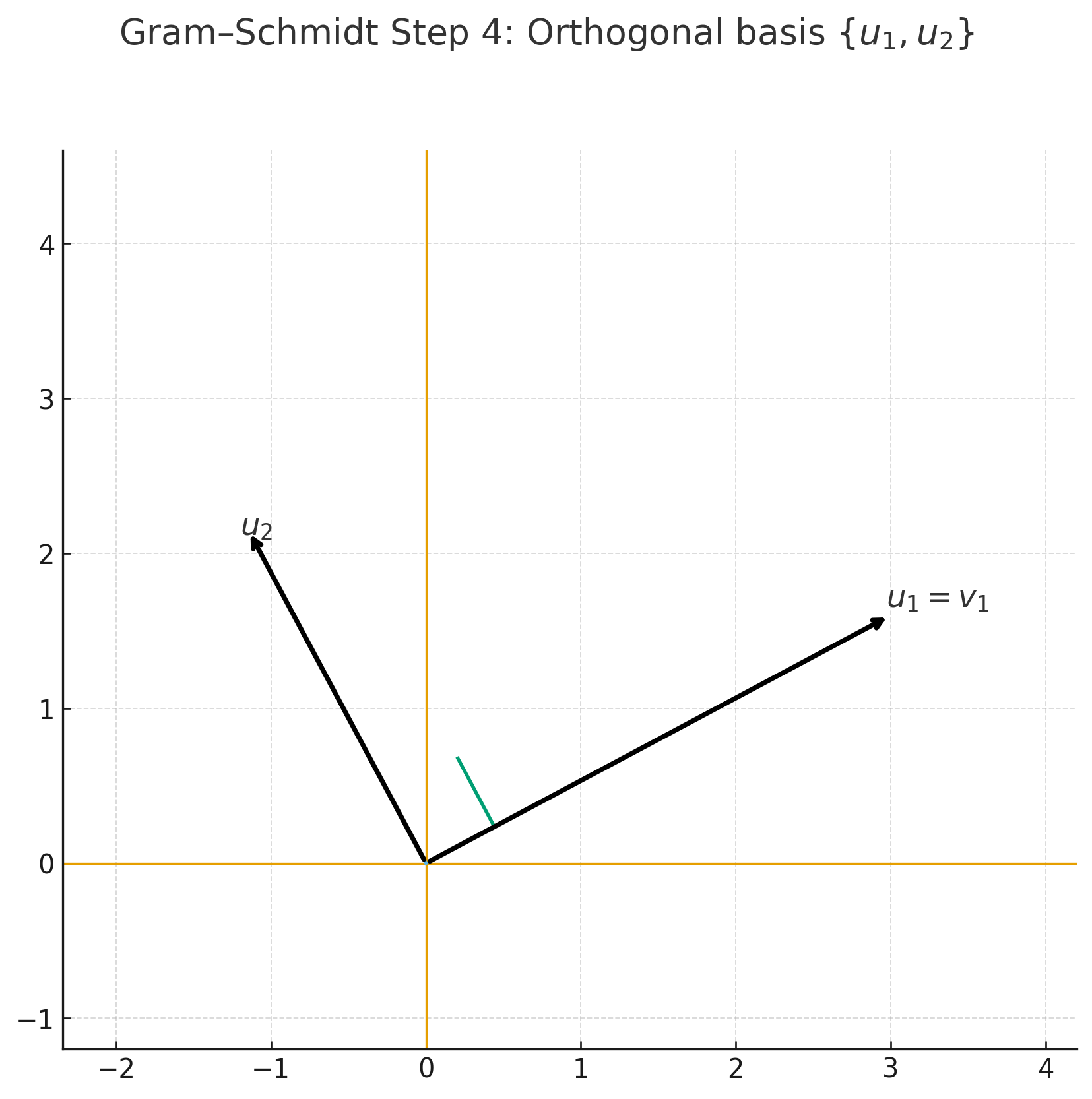 Step 4 — 직교 기저 \(\{u_1, u_2\}\) |
👉 가우스 환원 (정수배만 허용)
- 격자 기저를 더 수직에 가깝게 만드는 방법.
- $v_2$에서 $v_1$의 정수배를 반복해서 빼주면, 점점 짧고 수직에 가까운 벡터가 만들어진다.
- 이 과정을 번갈아 적용하면, 결국 “더 좋은 기저”를 찾을 수 있다.
- 가우스는 2차원에서 이 환원이 항상 유한 번 안에 끝난다는 것을 증명했다.
👉 차원 확장과 난이도
- 3차원, 4차원에서도 비슷한 아이디어로 기저를 개선할 수 있다.
- 하지만 차원이 커질수록 계산량이 기하급수적으로 증가한다.
- 결국 고차원 격자에서 SVP를 푸는 문제는 NP-hard임이 1997년에 증명되었다.
3) Geometry of Numbers: Lattices (3)
- Hardness of SVP
- SVP는 NP-hard로 알려져 있음 → 고차원 격자에서는 효율적 해법 없음
- 하지만 수학자들은 “격자점의 최소 길이 벡터는 어느 정도일까?”라는 질문을 오래 연구함
📘 Minkowski의 통찰
- 격자의 볼륨 (Det)
- 기저 벡터들이 만드는 평행사변형/평행육면체의 부피는 격자에 대한 불변량이다.
- 기저를 $v_1, v_2$로 잡든, $v_2, v_3$로 잡든 $\det(L)$ 값은 변하지 않는다.
- 직교 기저로 생각해보기
- 만약 $n$차원에서 모든 기저 벡터가 서로 직교하고, 길이가 모두 $\ell$이라면,
\(\det(L) = \ell^n \;\;\Rightarrow\;\; \ell = \det(L)^{1/n}\) - 따라서 최소 벡터의 길이는
\(\lambda_1(L) \leq \det(L)^{1/n}\)
정도일 것이라 직관할 수 있다.
- 만약 $n$차원에서 모든 기저 벡터가 서로 직교하고, 길이가 모두 $\ell$이라면,
- Minkowski의 정리
- 실제 일반 격자에서는 기저가 직교하지 않으므로, 위 직관보다 더 넉넉한 상한이 필요하다.
- Minkowski는 다음을 증명했다:
\(\lambda_1(L) \leq \sqrt{n}\,\det(L)^{1/n}\) - 즉, 최소 벡터의 길이는 격자의 부피(det)와 차원(n)에 의해 제약된다.
- 고차원에서는 $\sqrt{n}$보다 더 좋은 값이 알려진 경우도 있지만, $n \geq 10$ 이상에서는 여전히 정확한 상한이 미해결 문제다.
- 수학 문제를 다루는 세 가지 질문
- Existence (존재성): 해가 존재하는가?
- Uniqueness / Number (유일성·개수): 하나인가, 여러 개인가?
- Computability (계산 가능성): 실제로 계산 가능한가?
📘 LLL 알고리즘
- 배경
- Shortest Vector Problem (SVP)는 NP-hard → “계산 가능성”에 대한 해답이 필요하다.
- 아이디어
- 짧은 벡터를 찾으려면 더 좋은 기저(직교에 가까운 기저)가 필요하다.
- Gram–Schmidt 정규화는 실수 계수를 사용해야 해서 정수 격자에는 그대로 적용 불가
- LLL(1982)은 Gram–Schmidt를 기반으로 하되, projection coefficient \(\mu_{i,j} \;=\; \frac{\langle b_i,\, b_j^* \rangle}{\langle b_j^*,\, b_j^* \rangle}\) 를 계산한 뒤, 이를 가장 가까운 정수로 반올림하여
\(b_i \;\leftarrow\; b_i - \lfloor \mu_{i,j} \rceil \, b_j\) 형태로 기저를 반복 조정한다. - 이렇게 해서 완전히 직교는 아니더라도, 짧고 서로 덜 기울어진(nearly orthogonal) 기저를 구성할 수 있다.
- 결과
- $n$차원 격자에 대해,
\(\|v\| \leq 2^{(n-1)/4}\,\det(L)^{1/n}\)
이하의 길이를 갖는 벡터를 항상 찾을 수 있다. - 특히 낮은 차원($n \leq 17$)에서는 실제 shortest vector까지 정확히 찾아준다.
- $n$차원 격자에 대해,
- 의의
- NP-hard 문제에 대한 최초의 근사 해법.
- 지금도 수학자들이 “아름다운 알고리즘”으로 꼽는다.
- 현대 격자 기반 암호의 안전성 분석과 구현에서 핵심 도구로 활용된다.
- 격자 문제와 암호학
- 1980s: LLL의 등장으로 격자 문제가 “풀릴 수 있다”는 큰 기대
- 1990s: 하지만 $n$이 커지면 근사만 가능, 1996–97년에 SVP, CVP의 NP-hard성 증명
- 이 어려움은 암호학적 전환점이 되었음 → 격자 기반 암호(PQC)의 출발점
- 하지만 초기 격자 암호(예: Knapsack)는 LLL로 쉽게 깨짐
- 이유: NP-hard = 평균적으로 어렵다 는 아님
- 격자는 hard instance는 존재하지만, 대부분은 쉽게 풀림
- 비교:
- 이산로그 문제: self-reducible → 평균적으로 어렵다
- 인수분해 문제: 일반적으론 쉽지만 특수 구조(소수 곱)일 때 어려움 → RSA 기반
- Lattice: hard instance는 있지만 비율이 낮음
4) Geometry of Numbers: Lattices (4)
📘 Ajtai (1996–98): SIS 문제
- SIS (Small Integer Solution) 문제 제안
- 격자 문제 중 처음으로 average-case에서도 어렵다는 사실을 증명
- 즉, 무작위 인스턴스도 본질적으로 어렵다는 걸 보여줌
- 이로써 격자 문제를 기반으로 암호학을 설계할 수 있다는 가능성이 열림
- Regév (2003): LWE (Learning With Errors)
- $b = As + e \pmod{q}$ 꼴의 문제 정의 ($A$: 행렬, $s$: 비밀 벡터, $e$: 작은 에러)
- 에러가 없으면 단순 선형 방정식 → 매우 쉽게 풀림
- 하지만 작은 에러 $e$가 추가되면 문제는 급격히 어려워진다.
- LWE는 worst-case 격자 문제 → average-case LWE 문제로의 reduction이 존재
- 즉, 최악의 경우 어려우면 평균적으로도 어렵다는 것
- 이 reduction은 CVP(Closest Vector Problem) 등과의 연관 속에서 증명됨
- 의의
- Ajtai의 SIS → Regév의 LWE로 이어지며, NP-hard 격자 문제의 난이도가 실제 암호학적 안전성으로 연결됨
- 하지만 초기 LWE 암호는 파라미터(키 사이즈 등)가 너무 커서 실용성이 낮았다.
- 이후 최적화 연구를 거쳐 오늘날 PQC 표준의 기반이 됨
5) PKE from LWE
- 비밀키 암호 (대칭키 관점)
- 키 생성: $s \in \mathbb{Z}_q^n$
- 암호화: \(\text{Enc}_s(m) = (b, \langle b, s \rangle + e + m)\)
- $e$: 작은 노이즈, $m$: 메시지
- $v_i = \langle b_i, s \rangle + e_i$
→ 내적 후 작은 에러를 더해 메시지를 숨긴 것
- 공개키 암호 (Regév, 2005)
- 아이디어: “0의 암호화”를 여러 개 공개 → 그 조합에 $m$을 더해 새로운 암호문 생성
- 성질: $\text{Enc}_s(0) + m = \text{Enc}_s(m)$, 여러 개를 조합해도 여전히 0의 암호문
- 구체적 구성
- 공개키: $B, v = Bs + 2e$
- 암호화: $(c_1, c_2) = (rB, rv + m)$
- 복호화: $c_2 - c_1 s \equiv m + 2re \pmod{q}$
→ 작은 노이즈 무시하고 $m$ 복원
- 한계
- 안전성을 보장하려면 “0의 암호문”을 매우 많이 공개해야 함 (수십만~백만 개)
- 이는 Leftover Hash Lemma로 분석됨
- 초기 LWE 암호는 공개키 크기가 지나치게 커지는 단점이 있었음
📘 Leftover Hash Lemma
- 선형 결합된 분포가 “랜덤 분포와 거의 같다”는 것을 수학적으로 보임
- 기준: 통계적 거리 (Statistical distance ≈ 0)
- 단점: Lemma를 적용하려면 $B$의 크기가 매우 커야 함 (수십만~백만)
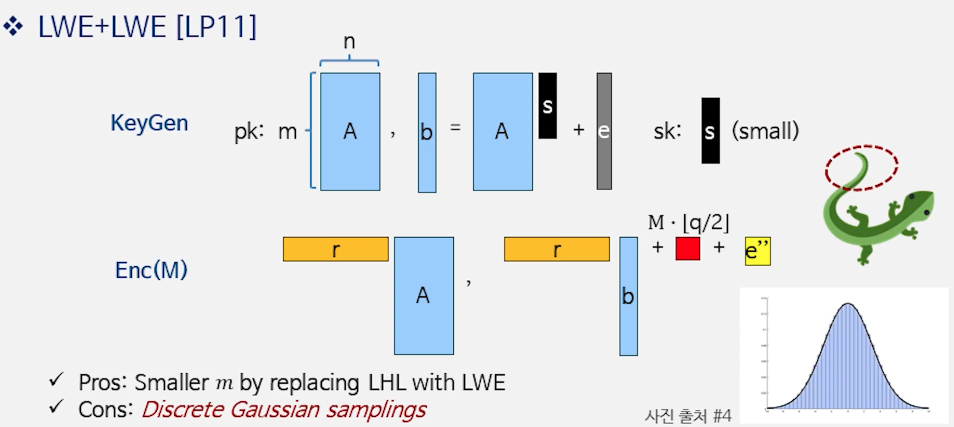
6) LWE + LWE [LP 11]
- 아이디어
- 공개키: $(A, b=As+e)$, 여기서 $e$는 작은 오류(이산 가우시안 등)
암호화: 무작위 $r\in{0,1}^m$로
\[c_1 = rA,\quad c_2 = rb + \left\lfloor \frac{q}{2} \right\rfloor m + e'\]- 문제: $c_1=rA$가 $A$의 행들의 짧은 선형결합이어서, 어떤 행 조합(= $r$)을 썼는지 정보가 새어 나갈 수 있음
- 개선: Lindner–Peikert (2011)
$c_1$에도 추가 잡음 $\hat e$를 주어
\[c_1 = rA + \hat e,\quad c_2 = rb + \left\lfloor \frac{q}{2} \right\rfloor m + e''\]로 만들어, “어느 행을 골랐는가”라는 문제가 다시 LWE-류의 난이도로 귀결되게 설계
핵심 효과: Leftover Hash Lemma (LHL)로 많은 샘플을 공개하지 않고도 작은 $m$으로 안전성 확보
📘 가우시안(이산) 오류와 샘플링
- 증명상 이산 가우시안(또는 서브가우시안) 오류가 표준적 가정
- 예: 표준편차 $\sigma=1$이면 $|X|\le 1\sigma$ 약 68.3%, $2\sigma$ 약 95.5%, $3\sigma$ 약 99.7%
- 구현 난이도: 정확한 이산 가우시안 샘플링은 사전 테이블(CDT/Knuth–Yao) 또는 rejection으로 처리 → 연산/메모리 비용 증가
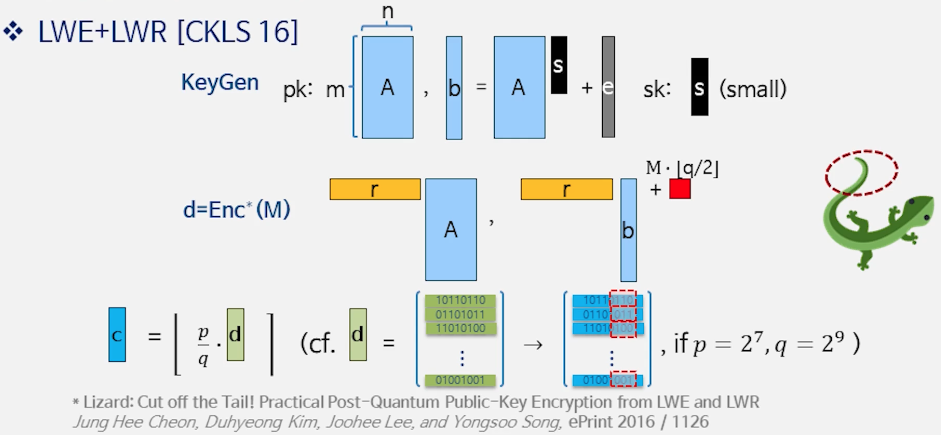
7) LWE + LWR [CKLS 16]
- 후속 아이디어: “Cut off the Tail”
- 관찰: $v_i=\langle b_i,s\rangle+e_i+m$에서, $e_i$가 $k$비트 규모면 하위 $k$비트는 정보가 거의 없다.
→ 하위 비트 truncate(rounding) 로 처리 - 더 나아가, 무작위 노이즈를 따로 샘플링하지 않고 라운딩 자체로 잡음을 유도하는 LWR로 대체
(라운딩은 결정론적이지만, 결과적으로 작은 오차를 주는 효과. $|\mathrm{round}(x)-x|\le q/2^{k+1}$)
- 관찰: $v_i=\langle b_i,s\rangle+e_i+m$에서, $e_i$가 $k$비트 규모면 하위 $k$비트는 정보가 거의 없다.
- 보안/파라미터 직관
- 라운딩만 쓰면 LWE와 분포가 조금 달라져서(carry 등) reduction 경계가 느슨해진다.
→ 이를 보완하려면 더 많이 자르기(큰 $k$) 또는 더 큰 모듈러 $q$가 필요 - 보안은 LWE 난이도에의 리덕션(모듈러스 스위칭 + 라운딩 분석)으로 제공
- 라운딩만 쓰면 LWE와 분포가 조금 달라져서(carry 등) reduction 경계가 느슨해진다.
- 장점
- 가우시안 샘플링 불필요 → 구현 단순화 및 암호화 속도 향상
- 실제 구현에서 키/암호문 크기 대비 효율이 크게 개선
8) Learning with Rounding (LWR) Problem
- 정의
- LWE: $b_i = \langle a_i, s \rangle + e_i \pmod{q}$
- LWR: $b_i = \left\lfloor \tfrac{p}{q} \langle a_i, s \rangle \right\rfloor$
- 작은 노이즈 대신 라운딩(truncation)을 사용
- 핵심 결과
- LWR도 안전함 (LWE로의 reduction 존재)
- 조건: $q$가 충분히 크거나 $m$이 작은 경우
- 구현적으로는 Gaussian 샘플링 없이 효율적
📘 왜 안전한가?
- LWE: “노이즈를 더하고 하위 비트를 버림”
- LWR: “그냥 하위 비트를 버림”
- 두 경우 모두 상위 비트만 정보가 남고 하위 비트는 무의미
- 따라서 안전성이 동일하다고 증명됨
9) Advantages of LWR Assumption
- 기존 LWE 암호화는 ciphertext가 크고, 보안 증명을 위해 가우시안 샘플링이 필요했음
- LWE+LWR(Lizard)에서는 하위 비트를 잘라내는 방식으로 가우시안 샘플링을 제거
- 장점:
- 더 작은 ciphertext
- 더 빠른 암호화 (구현 단순화)
10) Performance & Efficiency
- 격자 기반 암호는 이론적으로 안전성에서 큰 장점을 가지지만,
실제 구현에서는 속도, 키/사이퍼텍스트 크기, 효율성 측면에서 trade-off가 존재한다.
📘 Comparison with RSA and NTRU
- 성능
- 암호화 속도: RSA보다 약 3배 빠름
- 복호화 속도: RSA 대비 200배 이상 빠름 → 실제로 경량화 달성
- Trade-off
- 사이퍼텍스트 크기는 약 2배 커짐
- 타원곡선 기반 암호(ECC)와 비교하면 불리한 점 존재
📘 Recent Implementation
- 성능 개선
- Lizard.CCA: 32-byte 메시지 암호화에 0.020 ms
- RLizard.CCA: 0.036 ms (Category 1, AES-128 수준 양자 보안)
- Key/CT 사이즈
- Lizard.CCA: 공개키 1.8MB (압축 시 0.3MB), CT 0.98KB
- RLizard.CCA: 공개키 4.1KB (압축 시 1.3MB), CT 2.2KB
- 링 구조(RLWE)를 사용하면 더 작은 키 사이즈 가능
- 해석
100k cycles ≈ 0.036 ms(3GHz CPU 기준) → 매우 빠른 연산- Category 1 보안 = AES-128과 동등한 양자 보안 수준
📘 Standardization & Security Margin
- 제안(Proposal)
- 연구팀이 NIST 등 표준화 기구에 알고리즘 사양/코드/보안분석을 제출
- 채택(Selection)
- 여러 후보 중 라운드 진출(1차·2차·3차) 등 표준 후보군으로 선별
- 표준화(Standardization)
- 최종 선정 후 국제/국내 표준 문서로 확정되어 공공·산업에서 공통 사용
- 128비트 보안
- 공격에 대략 $(2^{128}$) 연산이 필요하다는 뜻 (= AES-128급)
- NIST 표현으로는 보통 Category 1 (양자·고전 공격자 모두 고려했을 때 AES-128을 깨는 것과 동일한 난이도) 수준과 대응
- Security Margin(여유분)
- “향후 더 강한 공격”을 대비해 목표 보안보다 여유 비트를 더 줌
- 예: $(128\text{비트} + 10\text{비트}$) 설정 ⇒ 더 큰 파라미터 (키/CT↑)가 필요
Security of Public-Key Cryptosystems
Published:
해당 포스트는 서울대학교 천정희 교수님의 암호론 강의를 기반으로 작성하였다. 이번 포스트에서는 ‘공개키암호의 안전성’에 대한 내용을 요약•정리하고자 한다.
1. 공개키암호의 안전성 개념 (Security of Public-Key Cryptosystems)
1) 공개키암호의 안전성 개념
- Targets
- One-wayness (OW): 역연산이 어려움 (hard to invert)
$\rightarrow$ 평문($e$)에서 암호문($c$)으로 갈 수 있지만 반대로는 불가하다!
(그렇지만 평문이 짝수인지 홀수인지 알 수 있다는 것을 알게 됨ㅠ) - Semantically Secure (Indistinguishable: IND): 부분 정보 노출 없음 (no partial information)
- 암호문 $c = E(m)$을 통해, 공격자가 평문 $m$에 대한 어떤 부분 정보도 추론할 수 없어야 한다.
- 즉, 암호문이 평문의 성질(예: 짝수/홀수, 길이, 특정 비트 값 등)을 드러내면 안 된다.
- 이를 만족할 때, 암호문은 평문에 대한 정보를 전혀 새지 않고 무작위처럼 보인다고 말한다. - Non-malleability (NM): 암호문으로부터 의미 있는 변형을 만들기 어려움
- $R$: 어떤 non-trivial relation (비자명한 관계)
- $E(M)$: 평문 $M$의 암호문
- NM조건: 공격자가 $E(M)$을 보고도 $E(R(M))$을 얻는 게 어렵다.
$\rightarrow$ 암호문을 변형해서 원래 평문과 관련된 다른 유효한 평문의 암호문을 얻을 수 없어야 한다.
$\Rightarrow$ Semantically Secure하지 않으면, Indistinguishable하지 않다!
- One-wayness (OW): 역연산이 어려움 (hard to invert)
📘 Indistinguishable 고차원 개념
- 정의
암호체계가 indistinguishable 하다는 것은 공격자가 두 개의 평문 $m_0, m_1$ 중에서
임의로 하나를 선택 후, 암호문 $E(m_b)$을 만들어서 $(m_0, m_1, E(m_b))$ 으로부터
$b$ 의 정보를 얻는 것이 어려워야 한다는 것을 의미한다.
- Attacks
- Passive attacks (Chosen Plaintext Attack: CPA)
- Active attacks (Chosen Ciphertext Attack: CCA)
2) Semantic Security (Indistinguisability: IND)
- 단계
- 공격자가 두 평문 $m_0, m_1$ 을 선택한다.
- 공격자는 무작위 비트 $b \in {0,1}$ 을 선택해서, 암호문 $c=E(m_b)$을 얻는다.
- 공격자는 $(m_0, m_1, c)$ 를 바탕으로 $b$를 추측한다.
- 공격자의 추측 $b’$ 가 실제 $b$와 같을 확률은 무작위 추측 수준($\frac{1}{2}$)을 유의미하게 넘지 않아야 한다.
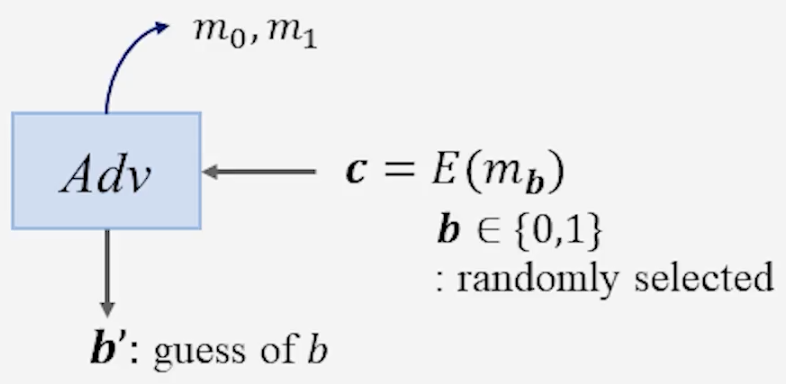
\(\therefore \Pr[b = b'] \leq \tfrac{1}{2} + \text{negl}(n)\) (여기서 $\text{negl}(n)$은 보안 매개변수 $n$에 대해 무시 가능한 값이다.)
3) Chosen Ciphertext Attack (CCA)
- CCA1 (Lunch time attack, Naor-Yung, ‘90)
- 공격자가 능동적 공격을 끝낸 후 암호문 $C_0$을 얻을 수 있는 상황
- CCA2 (Rackoff - Simon, ‘91)
- 공격자가 능동적 공격을 시작하기 전에 암호문 $C_0$을 얻을 수 있는 상황
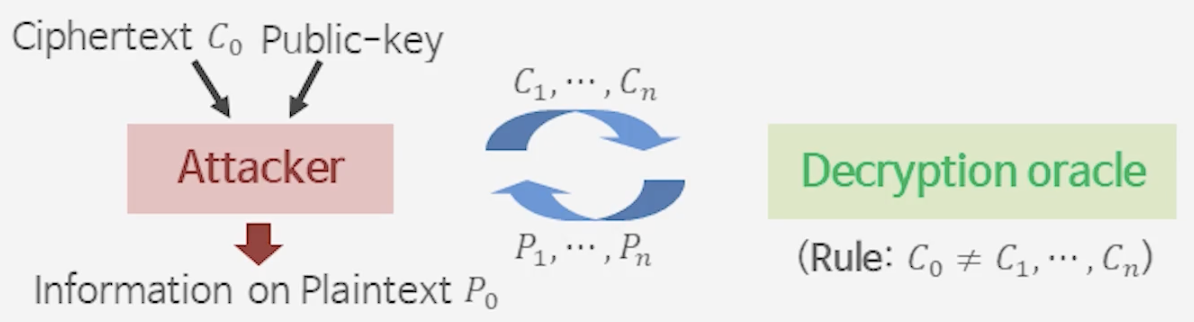
4) 공개키암호의 안전성 발전 역사
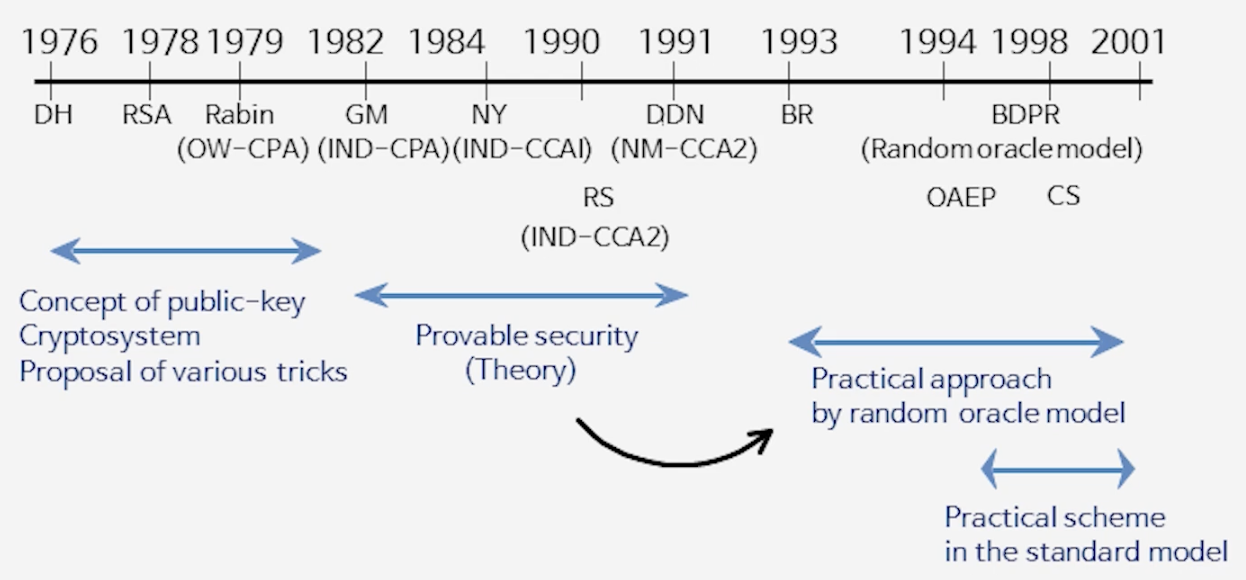
5) 가장 강력한 보안 (IND-CCA2) 암호체계 구성 방법
- Zero-Knowledge Proof 기반
- Dolev–Dwork–Naor (1991)
$\Rightarrow$ 비효율적 (Inefficient)
- 랜덤 오라클 모델 기반 (truly random function 가정)
- Bellare–Rogaway: OAEP (1994), PKCS#1–Ver.2 (1998)
- 대담한 가정: 해시 함수가 랜덤 함수와 구별 불가하다면 → 안전성 증명 가능!
- 물론 이 가정은 거짓. 해시 함수는 랜덤 함수처럼 작동하지만 실제로는 다르다.
📘 그럼에도 의미가 있었던 이유
- 그런 가정 위에서 RSA의 안전성을 처음으로 증명할 수 있었음
- 잘못된 가정을 출발점으로 했지만, 이후 점차 약한 가정을 사용하며 진짜 증명에 도달
- “틀린 가정이라도 증명 기법 발전의 촉매제 역할”을 했다는 점에서 큰 의의
- Fujisaki–Okamoto (1999), Pointcheval (2000)
- Okamoto–Pointcheval: REACT (2001)
$\Rightarrow$ 실용적 (Practical): 실제로는 무작위 함수 대신 일방향 함수(one-way functions)를 사용
- Bellare–Rogaway: OAEP (1994), PKCS#1–Ver.2 (1998)
- 랜덤 함수 없이도 가능한 실용적 구성
- 이산로그에 기반한 Cramer–Shoup (1998)
→ 표준 모델에서 처음으로 IND-CCA2 안전성을 만족하는 실용적 공개키 암호체계
- 이산로그에 기반한 Cramer–Shoup (1998)
6) Naïve RSA와 ElGamal의 안전성
- RSA는 malleable (변형 가능)하다.
📘 malleable 의미
RSA에서 $c = m^e \pmod{n}$ 일 때, \(2^{e} \cdot c \equiv (2m)^e \pmod{n}\)
→ 공격자는 원래 메시지 $m$을 몰라도, $2m$에 해당하는 새로운 암호문을 쉽게 만들 수 있다.
→ 즉, 암호문에서 평문과 연관 있는 다른 암호문을 생성할 수 있으므로 Non-malleability(NM)를 만족하지 못한다. - ElGamal (유한체 위에서 정의된 경우)
→ IND 보안(Indistinguishability)을 만족하지 않는다.📘 왜 IND가 깨지는가?
ElGamal 암호문은 $(g^r, m \cdot h^r)$ 꼴이다.
- 여기서 $g$는 생성원(generator), $r$은 랜덤 값.
- 하지만 공격자는 두 번째 성분을 통해 메시지가 $g$의 짝수 지수 꼴인지, 홀수 지수 꼴인지 판정할 수 있다.
→ 따라서 평문에 대한 일부 정보가 노출되어, 구별 불가능성(IND)이 깨진다.
- EC-ElGamal (타원곡선 기반)
→ IND-CCA2 보안을 만족하지 않는다.
📘 추가 설명: Generic Group vs Elliptic Curve Group
Generic Group Model (제네릭 군 모델)
공격자가 군의 원소를 다루지 못하고, 단지 "블랙박스 연산(곱셈·역원·동등성 검사)"만 가능하다고 가정
→ 이 모델에서는 ElGamal이 IND-CPA 보안을 만족한다.Elliptic Curve Group (타원곡선 군, 실제 구현)
실제 타원곡선 구조에서는 공격자가 곡선의 수학적 성질을 활용할 수 있음
즉, 공격자가 구체적인 타원곡선 구조를 활용한 공격도 가능해짐
→ 따라서 EC-ElGamal은 강한 보안(특히 IND-CCA2)을 만족하지 못한다.
7) Secure Conversion: 실용적이고 안전한 암호 만들기
Primitive 암호체계 (예: RSA, ElGamal)
→ 그대로 버리는 것이 아니라, 이를 기반으로 변환(conversion)을 적용할 수 있다.- 아이디어:
- primitive가 특정 조건 (예: trapdoor one-way, IND-CPA)을 만족하면
- 변환 상자(conversion)에 넣어 자동으로 IND-CCA2 안전한 암호체계를 얻을 수 있음
→ 이를 secure conversion이라 부른다.
- 연구적 의미:
- primitive의 안전성 증명 (예: trapdoor one-way, IND-CPA)는 비교적 쉽다.
- 하지만 IND-CCA 보안 증명/설계는 어렵다.
- 따라서 연구자들은 “IND-CPA 스킴 → conversion 적용 → IND-CCA2 스킴” 방식으로 접근했다.
📘 IND-CPA (Chosen Plaintext Attack 보안)
- 공격자가 원하는 평문 $m_0, m_1$을 선택한다.
- 암호문은 무작위로 선택된 $m_b$의 암호문 $c = E(m_b)$로 주어진다.
- 공격자의 목표: $b \in {0,1}$을 맞추는 것.
IND-CPA 보안 조건:
\(\Pr[b = b'] \leq \tfrac{1}{2} + \text{negl}(n)\) → 무작위 추측과 유의미하게 구별되지 않아야 한다.→ 암호문만 보고도 평문을 알아내기 어려워야 한다.
📘 IND-CCA2 (Chosen Ciphertext Attack 보안)
- 공격자는 복호화 오라클을 이용해 임의의 암호문 $c_1, \dots, c_n$을 복호화해볼 수 있다.
- 단, 목표 암호문 $c^*$ 자체는 복호화할 수 없다.
- 목표: $c^* = E(m_b)$에 대해 $b \in {0,1}$을 맞추는 것.
IND-CCA2 보안 조건:
\(\Pr[b = b'] \leq \tfrac{1}{2} + \text{negl}(n)\) → 복호화 오라클을 쓸 수 있어도 무작위 추측 수준 이상 맞출 수 없어야 한다.→ 암호문만 보는 게 아니라, 다른 암호문을 복호화해보는 강력한 능력을 줘도 여전히 평문을 알아내기 어려워야 한다.
2. ElGamal의 IND-CPA 안전성 (IND-CPA Security of ElGamal)
1) ElGamal의 IND-CPA 안전성 정의
- $G$: 소수 차수 $p$를 갖는 (순환) 가환군, 생성원 $g \in G$
- DDH 문제 (Decision Diffie–Hellman)
$\colon$ 주어진 $(g, g^x, g^y, g^z)$에 대해 $z \stackrel{?}{=} xy \pmod p$를 판정
📘 ElGamal과 DDH의 관계
**“ElGamal이 깨지면 DDH도 깨진다 → 따라서 DDH가 안전하면 ElGamal도 안전하다”
- Interactive Assumption (상호작용 가정)
- ElGamal의 안전성을 정의하려면 공격자(Adversary)와 도전자(Challenger)가
메시지를 주고받는 시나리오를 설정해야 한다. - 수학적으로 깔끔하게 표현하기 어려워, 공격자가 존재하지 않는다는 식으로만 보안을 표현할 수 있다.
- ElGamal의 안전성을 정의하려면 공격자(Adversary)와 도전자(Challenger)가
- Non-Interactive Assumption (비상호작용 가정)
- 반면 DDH 문제는 단순하다.
- 주어진 $(g, g^x, g^y, g^z)$가 Diffie–Hellman를 만족하는 지 판별하기만 하면 된다.
- 공격자와의 상호작용이 필요 없고, 문제 자체를 풀 수 있느냐 없느냐만 보면 된다.
2) ElGamal의 IND-CPA 보안 실험
- 도전자 $C$가 비밀키 $k \xleftarrow{$} \mathbb{Z}_p$를 뽑고 공개키 $g^k$를 만든다.
- 도전자 $C$는 공개키 $g^k$를 공격자 $A$에게 보낸다.
- 공격자 $A$는 두 평문 $m_0, m_1$을 선택해 도전자 $C$에게 보낸다.
- 도전자 $C$는 무작위 $r \xleftarrow{$} \mathbb{Z}_p$와 무작위 비트 $b\in{0,1}$를 뽑고
암호문 $c=(g^r,\; m_b \cdot (g^k)^r)$를 $A$에게 전달한다. - 공격자 $A$는 $b$를 추측해 $b’$를 제시한다.
(보안 조건: $\Pr[b’=b] \le \tfrac12 + \mathrm{negl}(n)$)
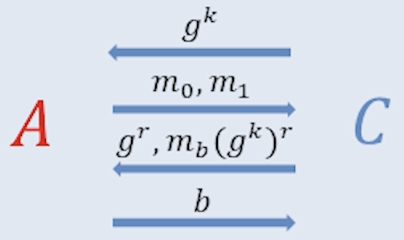
3) ElGamal의 IND-CPA 보안 실험 증명
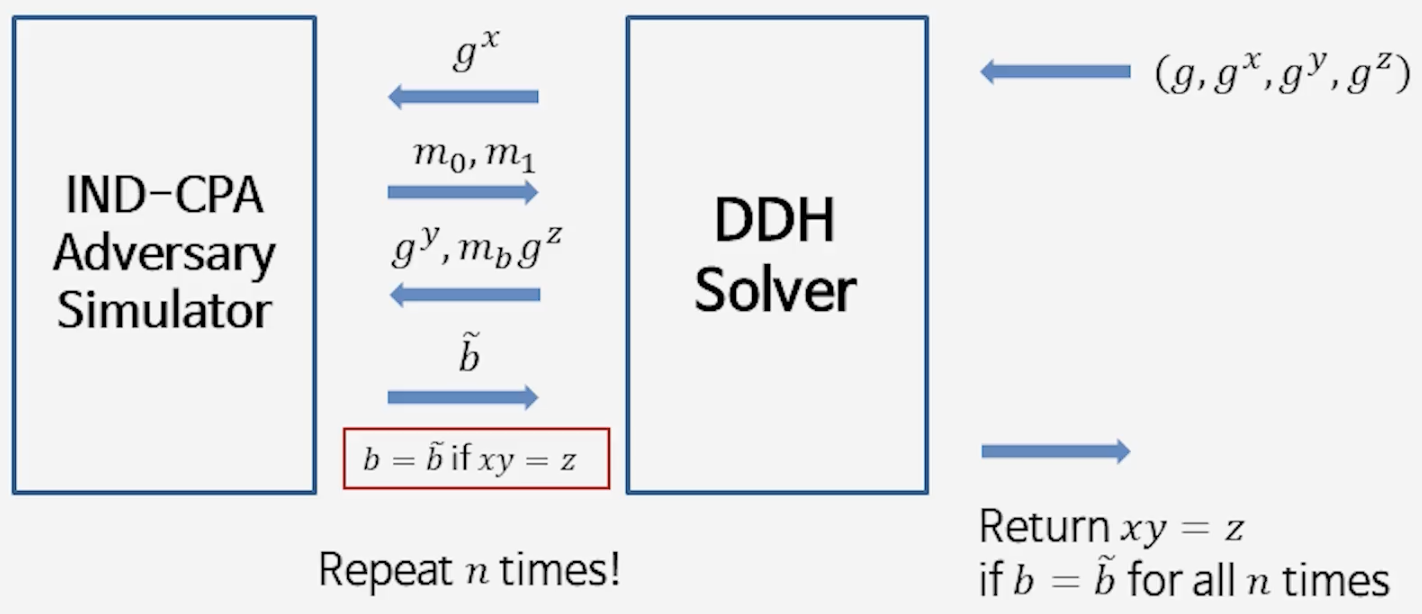
- 가정
- 공격자가 아주 가끔이라도 $b$를 잘 맞출 수 있다고 하자.
- (이득이 작아도 반복/증폭 기법으로 항상 잘 맞추는 공격자로 바꿀 수 있음.)
- DDH 문제와 연결
- 우리가 받은 문제: $(g, g^x, g^y, g^z)$
- 목표: $z = xy$인지 아니면 랜덤인지 판별
- 공격자 활용
- $g^x$ → 공개키처럼 전달
- $g^y$ → 난수 $r$ 대신 사용
- $g^z$ → 암호문의 두 번째 성분 자리에 넣음
- 판정 원리
- 만약 $z=xy$: 공격자가 받은 건 올바른 암호문
→ $b$를 잘 맞춤 → DDH = “예 (Yes)” - 만약 $z\neq xy$: 공격자가 받은 건 잘못된 암호문
→ 공격자는 랜덤처럼 동작 → $b$를 못 맞춤 → DDH = “아니오 (No)”
- 만약 $z=xy$: 공격자가 받은 건 올바른 암호문
- 반복 실험과 분포 판정
- 실제 증명에서는 단 한 번의 실행만으로 끝내지 않는다.
- 공격자가 무작위 추측(50%)보다 유의미하게 높은 확률로 $b$를 맞추는지,
여러 번 반복 실험을 통해 분포를 기준으로 판정한다.
📘 비유: 공격자를 시장에서 사온다?
- 가정
- ElGamal을 무너뜨릴 수 있는 공격자가 어딘가에 존재한다고 치자.
- 이 공격자는 아무 입력에나 작동하지 않고, CPA 실험 절차에서만 동작한다.
- 시장 비유
- 마치 “공격자를 파는 시장”에서 그런 컴퓨터를 하나 사왔다고 생각한다.
- 그 공격자는 우리가 준 공개키·평문·암호문 시나리오 안에서만 움직인다.
- 실제로 있는 건 아니지만, 사고실험(thought experiment)으로 가정한다.
- Reduction (귀속 아이디어)
- 우리가 진짜로 풀고 싶은 건 DDH 문제: $(g, g^x, g^y, g^z)$ 네 값이 주어졌을 때,
마지막 값 $g^z$가 정말 $g^{xy}$인지, 아니면 랜덤 값인지 구별할 수 있는지를 묻는 문제다. - 그런데 ElGamal 공격자를 블랙박스처럼 활용하면, 이 판별을 할 수 있다.
- 즉, ElGamal 공격자가 $b$를 잘 맞출 수 있다면 → $z=xy$인지 여부도 알아낼 수 있다.
- 우리가 진짜로 풀고 싶은 건 DDH 문제: $(g, g^x, g^y, g^z)$ 네 값이 주어졌을 때,
- 작은 이득도 괜찮다
- 공격자가 $b$를 무조건 잘 맞추지 않아도 된다.
- 무작위 추측보다 아주 조금이라도 잘 맞춘다면,
반복 실행과 증폭 기법으로 충분히 유의미한 공격자로 바꿀 수 있다.
✅ 핵심
- ElGamal 공격자가 있다면 → DDH 해결기가 만들어진다.
- DDH가 어렵다면 → ElGamal 공격자는 없다.
- 따라서 DDH가 안전하면 ElGamal도 IND-CPA로 안전하다.
3. RSA암호의 IND-CCA2 안전성 (IND-CCA2 Security of RSA)
1) RSA의 IND-CCA2 안전성 설명
- IND-CPA와의 차이점
- CPA에서는 공격자가 공개키와 암호문만 보고 $b$를 맞추는 실험을 한다.
- CCA2에서는 공격자가 복호화 오라클(Decryption Oracle)에 질문할 수 있다.
- 즉, 원하는 암호문을 입력하면 평문을 돌려받는 환경을 가정한다.
- 👉 오라클(Oracle)이란?
마치 신탁처럼, 우리가 질문(입력)을 던지면 그에 맞는 답(출력)을 돌려주는 가상의 상자를 말한다. 실제로 존재하지는 않지만, 보안 모델을 정의하기 위해 가정한다.
- 문제점
- DDH Solver는 비밀키 $x$를 모르기 때문에 직접 복호화를 해줄 수 없다.
- 하지만 공격자는 “복호화를 요청할 수 있다”는 조건 하에서만 동작한다.
- 따라서 Solver가 공격자에게 진짜 복호화를 해주는 척(시뮬레이션) 해야 한다.
- 결과
- 공격자는 실제로는 복호화한 결과물을 받지 못하지만, 마치 받는 것처럼 “착각”하게 된다.
- 이렇게 시뮬레이션을 만들어야만 CCA2 환경에서의 안전성을 증명할 수 있다.
- 따라서 IND-CCA2 보안 증명은 CPA보다 훨씬 어렵다.
2) OAEP (Optimal Asymmetric Encryption Padding)
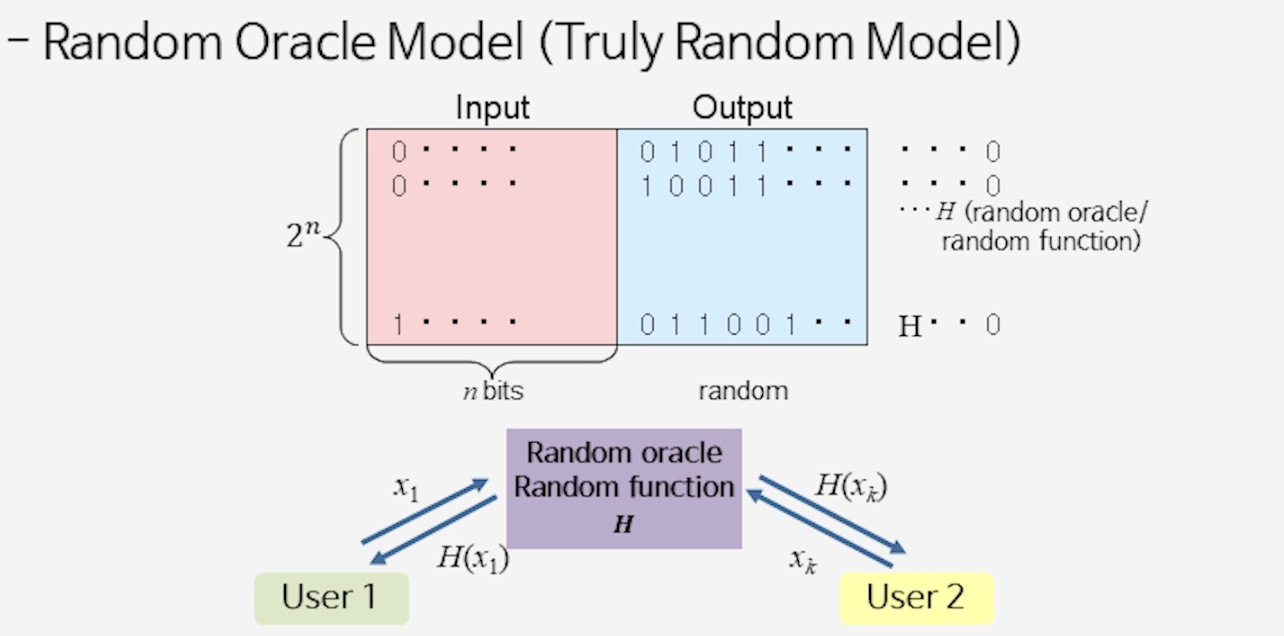
📘 랜덤 오라클(Random Oracle) 가정
- 해시 함수 $H$를 무작위 신탁(oracle)처럼 다룬다.
- 가정 조건
- 물어보기 전에는 $H(x)$ 값을 알 수 없다.
- 같은 입력 $x$를 넣으면 항상 같은 답 $H(x)$를 준다.
- 실제 해시는 계산 가능한 함수이므로 진짜 “랜덤 오라클”은 아니다.
- 하지만 증명을 위해 “랜덤 오라클처럼 동작한다”고 가정한다.
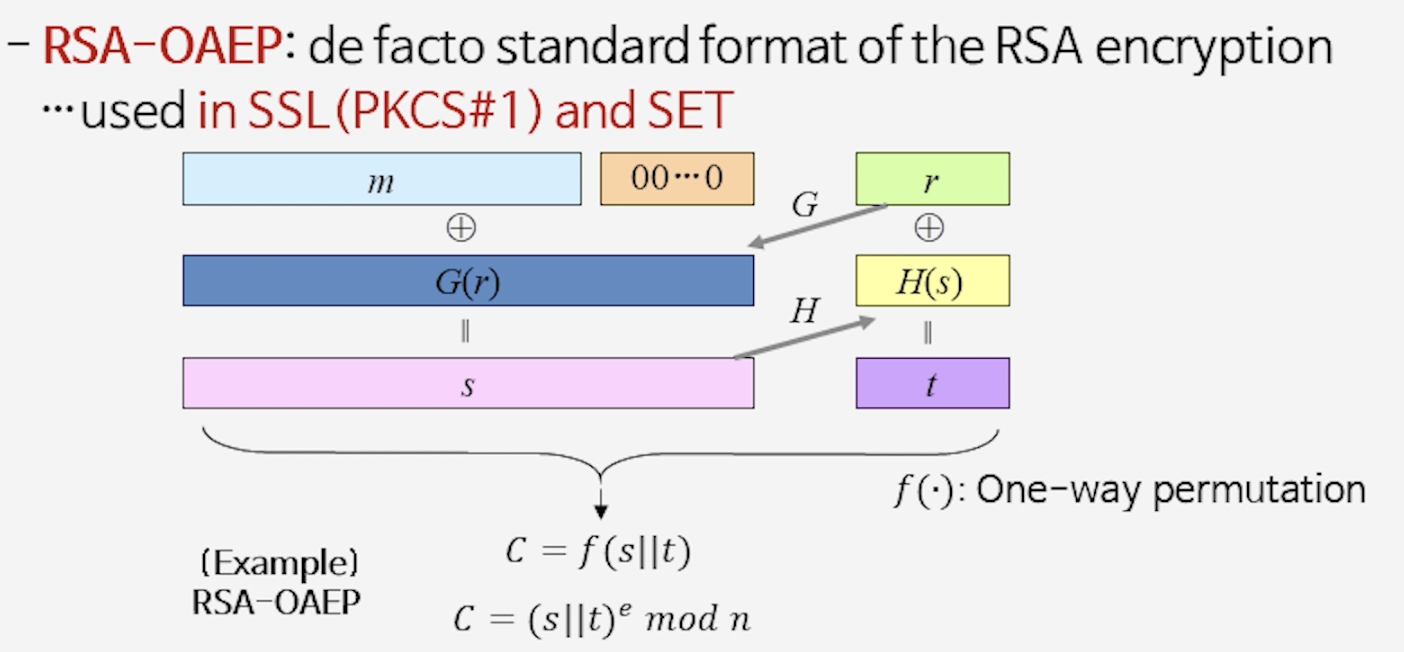
- 아이디어
- 평문 $m$에 무작위 값 $r$을 섞어 해시 함수 $G, H$를 적용하고,
결과를 다시 조합하여 $(s||t)$라는 블록을 만든 뒤 RSA로 암호화한다. - $f$: 일방향 함수 (예: $x \mapsto x^e \bmod n$)
- 결과 암호문: $C = f(s||t)$
- 평문 $m$에 무작위 값 $r$을 섞어 해시 함수 $G, H$를 적용하고,
- 특징
- $G, H$를 랜덤 오라클로 가정하여 증명을 진행한다.
- 이 padding 방식을 사용하면 RSA-OAEP라는 안전한 RSA 스킴이 된다.
- 실제로 PKCS#1 v2에 표준으로 채택되어 SSL, SET 등에서 사용되었다.
3) RSA-OAEP의 보안 증명 (랜덤 오라클 모델)
- 가정
- $f$는 일방향 함수 (예: RSA 지수승 모듈로 $n$).
- $H$는 해시 함수이지만, 증명에서는 랜덤 오라클로 취급한다.
- 증명 아이디어
- 만약 공격자가 RSA-OAEP를 구별할 수 있다면, 결국 $f$를 역산할 수 있다는 걸 보인다.
- 즉, 구별 가능성(distinguishability)이 곧 역산 가능성(invertibility)을 의미한다.
- 결론
- 랜덤 오라클 모델 하에서, RSA-OAEP는 IND-CCA2 안전성을 만족한다.
- 따라서 RSA에 padding을 잘 설계하면, 이론적으로도 안전성과 실용성을 모두 확보할 수 있다.
Public-Key Cryptography and RSA
Published:
해당 포스트는 서울대학교 천정희 교수님의 암호론 강의를 기반으로 작성하였다. 이번 포스트에서는 ‘공개키암호와 RSA’에 대한 내용을 요약•정리하고자 한다.
1. 공개키암호 (Public-Key Cryptography)
1) One-way Function
$x$가 주어졌을 때, $f(x)$를 계산하긴 쉽지만, $f(x)$가 주어졌을 땐 $f^{-1}(x)$를 계산하는 것은 어렵다.
$e.g.)$ 큰 수의 소인수분해 → $pq$ 계산은 쉽지만, $n=pq$ 일 때, $p$ 와 $q$ 를 찾는 것은 어렵다.🎯 깜짝 퀴즈 🎯
일방향 함수만 있으면 공개키 암호를 만들 수 있을까?
→ Open Problem
(단, 전자서명은 일방향 함수만 있어도 만들 수 있다는 것이 증명됨)
2) Trapdoor One-way Function
- 공개키 암호는 “누구나 암호화할 수 있고, 특정 비밀키로만 복호화할 수 있어야” 한다.
- 즉, 일방향 함수에 추가로 특별한 비밀 정보(Trapdoor Information, 일종의 열쇠 🔑)가 주어진다면, $y$가 주어졌을 때, $f^{-1}(y)$는 쉽게 계산할 수 있다.
3) Diffie-Hellman 키 교환
- 두 사람이 공개된 통신로를 통해 비밀 정보를 공유하는 방법
- 초기화 (변수 생성후 공개)
• 소수 $q$ ($q-1$ 이 큰 소수 약수를 가짐 - $e.g.) q=23, q-1=22=2 \times 11$)
• $q$ 보다 작은 자연수 $g$ - 과정
• Alice: 개인키 $a$, 공개키 $A = g^a \pmod{q}$
• Bob: 개인키 $b$, 공개키 $B = g^b \pmod{q}$
• Eve (도청자): $g^a, g^b$에서 $a, b$ 정보를 알아내는 것은 어렵다.
※ 비밀키 $a, b \in \mathbb{Z}_p \;\; (0 \leq a, b < p \;\text{ 또는 }\; -\tfrac{p}{2} \leq a, b < \tfrac{p}{2})$ 공통 비밀키 생성
• Alice는 $a, g^{b}$로 $g^{ab}$ 를 계산할 수 있다.
• Bob은 $b, g^{a}$로 $g^{ba}$ 를 계산할 수 있다.
※ 단, $g^{ab} = g^{ba}$ 이 성립하려면 연산 구조가 가환군(Commutative Group) 이어야 한다.📌 가환군(Commutative Group) = 교환 법칙이 성립하는 군
• 예제 1. $f_b \circ f_a(g) \overset{?}{=} f_a \circ f_b(g)$
• 예제 2. $(g^a)^b \overset{?}{=} (g^b)^a$
• 예제 3. $a,b$가 행렬일 때, $b(aga^{-1})b^{-1} \overset{?}{=} a(bgb^{-1})a^{-1}$안전성
• Eve는 $(g, g^a, g^b)$ 만으로는 $g^{ab}$ (공통 비밀 정보)를 계산하기 어렵다.
→ 이를 이산 로그 문제(Discrete Logarithm Problem) 라고 한다.🔎 왜 "이산 로그 문제"가 어려운가?
• 만약 모듈러 $p$ 없이 정수 지수승이라면:
$g^1, g^2, g^3, \dots$ 의 값은 계속 커지고, 대략 몇 번 곱했는지 추측할 수 있음
→ 여러 번 반복하면 로그 값(지수)을 조금씩 알아낼 수 있다.• 그러나 모듈러 $p$ 연산을 하면:
$g^a \pmod{p}$는 $0 \sim p-1$ 범위 안에서 뒤섞여(cycle) 나타남
→ 출력 값만 보고는 $a$의 크기를 추측할 단서가 사라진다.• 따라서 $y = g^a \pmod{p}$에서 $a$를 찾는 문제는 현재로써는 지수 시간이 걸린다.
📌 정리
• 정수 로그: 크기 비교로 추측 가능 → 쉽다.
• 이산 로그(mod p): 값이 wrap-around 되므로 추측 불가 → 어렵다.
• Diffie–Hellman 키 교환의 안전성은 바로 이 DLP의 난이도에 기반한다.🎯 깜짝 퀴즈 🎯
Discrete Logarithm 문제가 안전하면 Diffie-Hellman 문제는 어려울까?
혹은 Diffie-Hellman 문제를 풀 수 있다면 Discrete Logarithm 문제도 풀릴까?
→ Difficult Problem
[ DL과 DH의 관계 ]
• DL: $(g, g^a)$ 를 알 때 → $a$ 를 안다.
• DH: $(g, g^a, g^b)$ 를 알 때 → $g^{ab}$ 를 안다.
- 항상 성립: DL이 풀면 DH도 풀 수 있다.
→ 왜냐하면 $a$나 $b$를 알면 바로 $g^{ab}$를 계산할 수 있기 때문
- 미해결 문제: DH가 풀면 DL도 풀 수 있다.
→ 일반적으로는 아직 알려지지 않은 Open Problem
- 특별한 경우: $g$의 order = $p$인 경우,
• $\mathbb{DL}_p = \mathbb{DH}_p,$ $if$ $\exists$ an elliptic curve $E$ over $\mathbb{Z}_p$ $s.t.$ $|E(\mathbb{Z}_p)|$ is smooth.
→ 만약 어떤 타원곡선 $E$가 유한체 $\mathbb{Z}_p$ 위에 정의돼 있고, 그 점들의 개수 $|E(\mathbb{Z}_p)|$가 smooth하다면, DL 문제와 DH 문제가 동치라는 결과가 알려져 있다.
→ 충족하는 것을 찾는 데 걸리는 시간 $\neq$ 다항식 시간
※ $g$의 order(위수)란 "$g$를 계속 곱하다 보면 언젠가 처음 상태(1)로 돌아오는데,
그때까지 몇 번 곱해야 돌아오는지"를 의미한다.
→ 즉, 사이클 길이라고 이해하면 된다.
※ smooth란 큰 소수(prime number) 없이 작은 소수들만 곱한 것을 의미한다.
→ 예. 840 = $2^3 \cdot 3 \cdot 5 \cdot 7$
📌 쉽게 말하면,
- 평소엔 DL이 더 어려운 문제일 수도 있다.
- 하지만 특정 조건(타원곡선 위 점 개수가 smooth할 때)에서는
→ DH와 DL이 사실상 같은 난이도의 문제로 수렴한다.
- 초기화 (변수 생성후 공개)
4) PKC (Public-Key Cryptography) Schemes
- 1976 ~ 1984
- Diffie & Hellman / R.Rivest, A.Shamir, L.Adleman / Rabin scheme / Williams scheme /
McEliece scheme / Knapsack scheme
- Diffie & Hellman / R.Rivest, A.Shamir, L.Adleman / Rabin scheme / Williams scheme /
- 1985 ~ Current
- ElGamal scheme (Diffie & Hellman을 Encryption으로 바꾼 경우)
📌 Diffie–Hellman vs Ephemeral Diffie–Hellman
🔹 기본 Diffie–Hellman (DH)
- 한 번 생성한 개인키 $a, b$를 재사용 가능
- 공개키 $A = g^a, B = g^b$도 그대로 유지
- 키 합의는 안전하지만, Forward Secrecy(순방향 보안)는 보장되지 않음
(만약 개인키가 유출되면 과거 통신도 모두 복호화 가능)
※ Forward Secrecy: 장기 개인키가 유출되더라도, 과거의 세션 키와 통신 내용은 복호화되지 않도록 보호하는 성질
🔹 Ephemeral Diffie–Hellman (Ephemeral DH, ECDHE)
- Ephemeral = 세션마다 새로운 개인키 생성
- 각 세션의 $A = g^a, B = g^b$ 가 사실상 퍼블릭 키(public key) 역할
- 세션이 끝나면 키를 버리므로, Forward Secrecy 보장
(개인키가 유출돼도 과거 세션은 안전) - 실제로 HTTPS (TLS/SSL)에서 많이 사용됨
📌 핵심
- “Ephemeral Diffie–Hellman을 쓰면, 그때그때의 공개키$(A, B)$가
바로 퍼블릭 키로 기능한다.” - 즉, DH 자체가 일시적인 공개키 암호 시스템이 되는 셈이다.
- Key Generation (KG): secret key (sk) = $b$, public key (pk) = $g^b$, ephemeral key = $r$
- 암호화 (Encryption)
• Alice가 메시지 $m$을 보낼 때, 임의의 $r$를 선택
• 암호문 = $(g^{r}, (g^{b})^r*m)$ → $g^{rb}$는 Bob의 공개키 $g^b$와 Alice의 $r$를 조합해서 생성 - 복호화 (Decryption)
• Bob(수신자): 개인키 $b$를 사용해 $g^{rb}$ 계산
• 복호문 = $m = \dfrac{m \cdot g^{rb}}{g^{rb}}$ 로 원문 복원
🔐 Encryption 구조
\(\mathrm{Enc}_{pk}: \mathbb{Z}_p \longrightarrow G \times G\)
\(m \longmapsto (g^r,\; g^{rb}\cdot m)\)• 여기서 $pk = g^b$, $b$: Bob의 개인키, $r$: Alice가 매 메시지마다 선택하는 난수
• ElGamal의 $G$는 “mod $p$에서의 곱셈군” $\mathbb{Z}_p^*$ 을 뜻한다🎯 깜짝 퀴즈 🎯
Q. ElGamal 암호화에서 sk = $b$, pk = $g^{b}$ 일 때,
• \(\mathrm{Enc}_{pk}: \mathbb{Z}_p \longrightarrow G \times G\)
• \(m \;\mapsto\; (g^r,\; g^{rb}\cdot m)\)
→ 복호화하기 위해서 필요한 정보는 무엇일까?A. 바로 Bob의 개인키 $b$ 이다.
$(g^r, g^{rb}\cdot m)$에서 $m$을 되찾으려면 $g^{rb}$를 알아야 하고,
이를 계산할 수 있는 유일한 정보가 $b$ 다.→ 따라서 $b$ 가 Trapdoor (비밀 열쇠) 역할을 한다.
⚠️ 단, 그렇다 해서 Trapdoor One-way Function 은 아니다.
→ 왜냐하면 ElGamal은 항상 같은 $f(x)$를 내는 고정된 함수가 아니라,
매번 임의의 $r$을 뽑아 다른 출력이 나오는 확률적 암호화 방식이기 때문이다.
즉, 수학적 함수라기보다는 암호화 스킴 전체에서
“거꾸로 갈 수 있게 해주는 비밀키”라는 의미로 트랩도어처럼 동작한다.🔑 정리 🔑
• Trapdoor One-way Function
→ “일방향만 쉽다.” (단, 비밀 정보(Trapdoor)가 있으면 거꾸로도 쉽다.)• 공개키 암호 (PKC)
→ “누구나 공개키로 암호화는 쉽게 할 수 있지만, 복호화는 어렵다.”
(단, 비밀키가 있으면 복호화가 쉽다.”)∴ 즉, 구조적으로 보면 공개키 암호(PKC) ≈ Trapdoor One-way Function이다.
→ 다만 수학적으로 정확히 동치 라기보다는,
PKC가 성립하려면 TOWF가 존재해야 한다는 의미에서 개념적 동치로 본다. - Elliptic Curve based scheme / Hidden Field Equations / Lattice Cryptography /
Non-abelian group Cryptography / Fully Homomorphic Encryption
- ElGamal scheme (Diffie & Hellman을 Encryption으로 바꾼 경우)
- Hard Problems for PKC
- Integer Factorization Problem (IFP)
• 큰 수 $n = pq$ 를 소인수분해하는 문제
• 관련: Quadratic Residuocity Problem - Discrete Logarithm Problem (DLP)
• $y = g^x \pmod p$에서 $x$를 구하는 문제
• 확장: Generalized DLP (Elliptic Curve, Hyperelliptic Curve, Class Field) - Linear Code Decoding
- Multivariate Equations
• 여러 변수에 대해 2차 이상의 다항식을 푸는 문제
• 일반형:
\(\begin{cases} f_{1}(x_{1}, ..., x_{n}) = a_{1} \\ f_{2}(x_{1}, ..., x_{n}) = a_{2} \\ \vdots \\ f_{n}(x_{1}, ..., x_{n}) = a_{n} \end{cases}\)
→ 1차(선형)일 경우, 가우스 소거법으로 $O(n^3)$ 안에 풀림
→ 2차 이상일 경우, NP-hard (실질적으로 매우 어려움)
• 관련: Hidden Field Equations, Isomorphism of Polynomials - Nonabelian Group (비가환군)
• Conjugacy Problem (켤레 문제): $a, b$가 주어졌을 때 $x^{-1}ax = b$인 $x$를 찾는 문제
• Decomposition Problem: 주어진 원소를 이루는 생성자들의 곱으로 분해하는 문제
※ 다만, 행렬군에서는 다항 시간 내로 풀려서, Braid Group(꼬임군) 등 다른 구조 사용 - Lattice 기반 문제
• SVP (Shortest Vector Problem): 주어진 격자에서 가장 짧은 벡터 찾기
• CVP (Closest Vector Problem): 주어진 점에 가장 가까운 격자 벡터 찾기
• 파생 문제들:
• Learning with Errors (LWE): $y = Ax + e \pmod q$에서 $x$를 찾는 문제 (작은 오류 $e$ 포함)
• Approximate Common Divisor (ACD): 약간의 노이즈가 있는 공약수 문제
→ 다만, 아직까지 NP-hard 문제를 기반으로 한 암호 스킴은 실용적으로 설계하진 못함
- Integer Factorization Problem (IFP)
📚 참고 자료 모아보기
1) 공개키 암호가 생겨난 이유
대칭키 암호(Symmetric Cryptosystem)의 한계
• 모든 통신 쌍이 서로 다른 비밀키를 공유해야 안전함
• 참가자 수가 $n$일 때 필요한 키 개수는 조합으로 계산됨: $\binom{n}{2} = \frac{n(n-1)}{2}$.
• 예: $n = 100 → 4,950$개의 키 필요
• 규모가 커질수록 키 관리가 폭발적으로 어려워짐발명 동기
• “비밀키를 미리 공유하지 않고도 안전하게 통신할 수 없을까?” → Diffie & Hellman의 아이디어
• 여기서 나온 개념이 바로 공개키 암호(PKC)공개키 암호의 혁신
• 공개키: 누구나 알 수 있음 → 암호화에 사용
• 비밀키: 당사자만 알고 있음 → 복호화에 사용
• 따라서 키를 미리 비밀리에 나눌 필요 없음 → 키 관리 문제 해결
2) Merkle’s Puzzle (1974)
- 최초로 “공개키 개념”을 제안한 시도
- Ralph Merkle, UC Berkeley 컴퓨터 보안 수업(1974) 제안
논문: Secure Communication over Insecure Channels (CACM, 1978)
Merkle Puzzle 아이디어
• 많은 퍼즐 중 하나를 선택해 해결 → 두 당사자만 공유하는 비밀키 획득
• 공격자는 퍼즐을 전부 풀어야 하므로 비용이 급격히 증가
• 다만 차이가 “1000배 수준(다항시간 내에 해결 가능)”이라 실제 보안성은 부족- 📌 교훈:
• 퍼즐 수를 늘리면 안전성은 기하급수적으로 증가
• 이 아이디어가 이후 Diffie–Hellman 키 교환으로 발전
3) 복잡도 (Complexity)
암호학은 결국 “쉽게 할 수 있는 연산과, 되돌리기 어려운 연산의 차이”에 의존한다.
연산 복잡도별 분류
• Linear: Addition, Subtraction
• Quadratic: Multiplication, Euclidean Algorithm, Modular Operations
• Cubic: Exponentiation, Matrix Multiplication, Gaussian Elimination
• Exponential: Factorization, TSP, Subset Sum, Lattice Problems📌 암호학적 핵심:
• 앞으로 계산은 쉽다 (다항 시간)
• 거꾸로 풀기는 어렵다 (지수 시간)
• RSA: 곱셈은 빠름, 소인수분해는 어렵다
• 격자 기반 암호: Lattice 문제의 난이도 활용P vs NP
• P: 다항 시간(Polynomial time) 안에 풀 수 있는 문제
• NP: 답이 맞는지 검증은 다항 시간 안에 가능(Non-deterministic Polynomial)
• P ⊆ NP, NP-complete = NP ∩ NP-hard
• 만약 P = NP라면, 현재 암호 시스템 대부분이 무너짐 (소인수분해, 이산 로그 등도 다항 시간에 풀리게 됨)
• 아직까지 전 세계적으로 해결되지 않은 컴퓨터 과학 최대 난제 중 하나.대표적인 어려운 문제들
• TSP (Traveling Salesman Problem)
도시 목록과 거리 정보가 주어졌을 때, 모든 도시를 정확히 한 번 방문하는 가장 짧은 경로를 찾는 문제• SSP (Subset Sum Problem)
정수 집합이 주어졌을 때, 어떤 부분집합의 합이 정확히 0이 되는지 묻는 문제• Integer Factorization
큰 수 (n = pq)를 소인수분해하는 문제 (RSA 안전성의 기반)
2. RSA (Rivest-Shamir-Adleman)
1) Prime
📘 Prime (소수)와 Euclid의 정리
- Prime (소수) 기본 개념
소수 정의
$p \geq 2$ 인 정수 $p$가 소수일 경우, \(a \mid p \;\Rightarrow\; a = \pm 1 \;\;\text{또는}\; \pm p\) 를 만족
→ 즉, 약수가 1과 자기 자신밖에 없음Irreducible (기약원)
$p = ab$ 를 인수분해했을 때, $a$ 또는 $b$ 중 하나가 단위원(unit, 즉 $\pm 1$) 일 때,
$p$ 를 기약원이라고 함 → 정수에선 기약원 = 소수라고 생각하면 됨
- Euclid의 정리
Euclid’s Lemma
\(p \mid ab \;\;\Rightarrow\;\; p \mid a \;\;\text{또는}\;\; p \mid b\)
→ 소수의 중요한 성질! (소수는 약간 “쪼갤 수 없는 블록”이라는 뜻)예시
• $p=5$, $ab = 20 = 4 \times 5$: $5 \mid (4 \times 5) \;\Rightarrow\; 5 \mid 5$ ✅
• $p=7$, $ab = 21 = 3 \times 7$: $7 \mid (3 \times 7) \;\Rightarrow\; 7 \mid 7$ ✅
• $p=6$, $ab = 6 = 2 \times 3$: $6 \mid (2 \times 3)$ 이지만 $6 \nmid 2$, $6 \nmid 3$ ❌ (합성수이므로 성립 ❌)무한 소수 정리 (Euclid)
• “소수는 무한히 많다.”
→ 만약 소수가 유한 개만 있다면, 그 소수들을 모두 곱한 뒤 +1을 하면 새로운 소수가 나타나
모순이 생긴다.
- Prime Number Theorem (소수 정리)
- $\pi(x)$ = $x$ 이하의 소수 개수
정리: \(\lim_{x \to \infty} \pi(x) / (\frac{x}{\ln x}) = 1\) → $x$ 이하 소수의 개수는 대략 $\dfrac{x}{\ln x}$
- 해석: “임의의 $x$ 근처의 수가 소수일 확률” ≈ $\dfrac{1}{\ln x}$
- 여기서 $\ln$은 자연로그 (밑 = $e$ ), 정확히는 $\dfrac{1}{(\text{자리수}) \cdot \ln 10}$
- 직관적으로 “10자리 수면 약 $\frac{1}{10}$, 100자리 수면 약 $\frac{1}{100}$ 확률”
-
예시
- $x = 10$ → 확률 $\frac{1}{\ln 10} \approx \frac{1}{2.3}$
- $x = 10^{10}$ (10자리) → 확률 $\frac{1}{(10 \ln 10)} \approx \frac{1}{23}$
- $x = 10^{100}$ (100자리) → 확률 $\frac{1}{(100 \ln 10)} \approx \frac{1}{230}$
- $x = 3^{100}$ (약 $10^{47.7}$ 크기의 수, 48자리 수 정도): \(\frac{1}{\ln(3^{100})} = \frac{1}{100 \ln 3} \approx \frac{1}{110}\)
→ 따라서 $3^{100}$가 소수일 확률은 약 $\frac{1}{110}$
- 일반 소수 정리의 오차항
- \(\pi(x) = \frac{x}{\ln x} + O\left(\frac{x}{\ln^2 x}\right)\)
→ 즉, 실제 소수 개수는 $\dfrac{x}{\ln x}$에 가깝지만, 그 차이는 대략 $\dfrac{x}{\ln^2 x}$ 정도 크기
- \(\pi(x) = \frac{x}{\ln x} + O\left(\frac{x}{\ln^2 x}\right)\)
- Riemann Hypothesis (리만 가설)
- 오차 항의 정밀도에 관한 주장
- $ \lvert \pi(x) - \mathrm{li}(x) \rvert < x^{\frac{1}{2}} \ln x $, where $\mathrm{li}(x) := \int_2^x \frac{1}{\ln t} dt = \frac{x}{\ln x}+O(\frac{1}{\ln ^{2}t})$
- 비교
- 일반 소수 정리: 오차항 $O\left(\tfrac{x}{\ln^2 x}\right)$
- 리만 가설: 오차항 $O\left(x^{\frac{1}{2}}\ln x\right)$ (훨씬 더 작음)
-
예시: $x = e^{100}$ 일 때,
- 일반 소수 정리 오차: \(\frac{e^{100}}{(\ln e^{100})^2} = \frac{e^{100}}{100^2}\)
- 리만 가설 오차: \((e^{100})^{\frac{1}{2}} \cdot \ln(e^{100}) = e^{50} \cdot 100\)
→ RH가 참이라면, 오차가 $ \frac{e^{100}}{100^2} $ 에서 $ e^{50}\cdot 100 $ 으로, 약 $ \frac{e^{50}}{100^{3}} \approx 3\cdot 10^{15} $ 배 대폭 줄어듦
📘 RSA의 수학적 기초 (Euler Phi Function, Fermat & Euler Theorem)
- Euler Phi Function
- 정의
$\varphi(n)$ = $[1,n]$ 범위 안에서 $n$과 서로소인 정수의 개수 - 성질
- $p$가 소수일 때, $\varphi(p) = p-1$
- $\varphi$는 곱셈적 함수 (Multiplicative):
→ 만약 $\gcd(m,n) = 1$ 이라면, $\varphi(mn) = \varphi(m) \cdot \varphi(n)$
- 공식
- $n = pq$ (두 소수 $p, q$ 일 때), $\varphi(pq) = (p-1)(q-1)$
- $n = p^k$ (소수 $p$의 거듭제곱일 때), $\varphi(p^k) = p^{k-1}(p-1)$
- 예시
- $\varphi(7) = 6$
- $\varphi(8) = 4$
- $\varphi(12) = 4$
- $\varphi(1457) = \varphi(31 \cdot 47) = \varphi(31)\varphi(47)$
$= (31-1)(47-1)$ = $30 \cdot 46 = 1380$ - $\varphi(1024) = \varphi(2^{10}) = 2^{10-1}(2-1) = 512$
- Fermat and Euler
- Fermat’s Little Theorem
- $p$가 소수일 때,
\(\gcd(a,p)=1 \;\;\Rightarrow\;\; a^{p-1} \equiv 1 \pmod{p}\)
- $p$가 소수일 때,
- Euler’s Theorem
- $a \in \mathbb{Z}_n^*$ 이면, \(a^{\varphi(n)} \equiv 1 \pmod{n}\)
- 따라서 임의의 정수 $a$에 대해, \(a^r \equiv a^s \pmod{n}, \quad \text{if } r \equiv s \pmod{\varphi(n)}\)
- $n$이 소수라면, $\varphi(n)=n-1$ 이므로, 페르마 소정리로 귀결된다.
📘 법(法)과 항등식
- 정의
- $(a-b)$ 가 $n$의 배수 $\Leftrightarrow a \equiv b \pmod{n}$
- $a$를 $n$으로 나눈 나머지$ \equiv a \pmod{n}$
- 예: $5 \equiv 2 \pmod{3}$, $5 \pmod{3} \equiv 2$
- 성질
- $a \equiv b \pmod{n}$ 이고 $c \equiv d \pmod{n}$ 이면,
- $a + c \equiv b + d \pmod{n}$
- $a - c \equiv b - d \pmod{n}$
- $ac \equiv bd \pmod{n}$
- $a \equiv b \pmod{n}$ 이고 $c \equiv d \pmod{n}$ 이면,
- 예시
- $1234 \times (56-78)$ 을 $3$으로 나눈 나머지는?
- $proof 1$
- $56 - 78 = -22 \equiv -1 \equiv 2 \pmod{3}$
- $1234 \equiv 1 \pmod{3}$
- $proof 2$
- $(1233+1) \times {(54+2)-(78+0)}$ $\equiv 1 \times (2-0) \equiv 2 \pmod{3}$
- 따라서 $1234 \times (56-78) \equiv 1 \times 2 \equiv 2 \pmod{3}$
- 최종 답: 나머지는 $2$
2) RSA 암호 (1978): Revest, Shamir, Adleman
- $n = pq$ (소수 $p, q$) 일 때, $\varphi(n)=(p-1)(q-1)$ 을 성립한다.
- Euler 정리: $n$과 서로소인 정수 $x$에 대해 $x^{\varphi(n)} \equiv 1 \pmod{n}$
- 준비 과정 (Alice)
- 소수 $p, q \rightarrow n = pq$
- 공개키 $(n,e)$: $n$보다 작은 정수 (이때, $\color{red}{e=2^{16}+1}$을 많이 사용)
- 비밀키 $(p,q,d)$: $de \equiv 1 \pmod{\varphi(n)}$
- 암호화(아무나): 암호문 $c \equiv m^{e} \pmod{n}$ 을 계산
- 복호화(비밀키 소유자 Alice만 가능):
- 암호문 $c$를 받아 $c^{d} = (m^{e})^d = m^{k\varphi(n)+1} \equiv m \pmod{n}$ 계산
(단, $m, n$이 서로소인 경우만 성립)
- 암호문 $c$를 받아 $c^{d} = (m^{e})^d = m^{k\varphi(n)+1} \equiv m \pmod{n}$ 계산
- 보안성: 공개키 $(n,e)$
- $n$을 인수분해 $\rightarrow p,q$ 안다 $\rightarrow \varphi(n)$ 안다 $\rightarrow e$에서 $d$ 계산 $\rightarrow c$에서 $m$ 계산
- 역은 성립하는 가?
- 복호화를 할 수 있다고 해서 비밀키 $d$를 알기 어렵다.
- $de \equiv 1 \pmod{\varphi(n)} \Leftrightarrow \varphi(n) | (ed-1)$
$\rightarrow \color{red}(ed-1)$을 안다고 해서 $\varphi(n)$을 안다는 보장이 없다!
3) Modular 지수승 계산 방법
- $d$의 생성: Extended Euclidean Algorithm $O(\log^{2}{n})$
- 지수승 계산: $a^{e}$ for $e = \sum_{i=0}^{t} e_{i} 2^{i}, \quad e_{i} \in {0,1}$
- 전개: \(e_{t}2^{t}+e_{t-1}2^{t-1}+ \cdots +e_{1}2^{1}+e_{0}\)
- 계산 구조: \((((a^{e_{t}})^{2}a^{e_{t-1}})^{2} \cdots )^{2}a^{e_{1}})^{2}a^{e_{0}}=a^{e_{t}2^{t}+e_{t-1}2^{t-1}+\cdots+e_{1}2^{1}+e_{0}2^{0}}\)
-
예시: $2^{26} \pmod{17}$
- $26 = (11010)_{2} = 2^{4}+2^{3}+2^{1}$
$\rightarrow 2^{26} = 2^{16} \cdot 2^{8} \cdot 2^{2}$ - $2^{1} \equiv 2 \pmod{17}$
- $2^{2} \equiv 4 \pmod{17}$
- $2^{4} \equiv 16 \equiv -1 \pmod{17}$
- $2^{8} \equiv (-1)^{2} = 1 \pmod{17}$
- $2^{16} \equiv (2^{8})^{2} \equiv 1^{2} = 1 \pmod{17}$
- $26 = (11010)_{2} = 2^{4}+2^{3}+2^{1}$
- 계산량 $\varphi(n)$
- $(t+1)$: $e$ 의 bit length | $wt(e)$: $e$의 Hamming weight
- $g$에 의해 $(t+1)$번 제곱, | $(wt(e)-1)$번 곱셈 필요
- $0 \le wt(e)-1 < |e| \Rightarrow$ 평균적으로 $|e|/2$ 성립
- $e.g.) |n|=1024 \Rightarrow$ 약 $1,536$번 곱셈 연산 필요
4) Fast Implementation in RSA
- Fast Multiplication
- Karatsuba Method
\(\colon (a_{0}+a_{1}x)(b_{0}+b_{1}x) = a_{0}b_{0}+(a_{0}b_{1}+a_{1}b_{0})x+a_{1}b_{1}x^{2}\) - Toom-Cook, FFT
- Montgomery Reduction
- Karatsuba Method
- Fast Exponentiation
- Sliding Window Method
- 밑(base)가 고정된 경우 Precomputation 활용
5) Fast Decryption Using CRT(중국인 나머지 정리)
- 목표: $M=C^{d} \pmod{n}$ where $n=pq$ 계산
- 계산 과정
- $C^{d} \pmod{p}$ 와 $C^{d} \pmod{q}$를 먼저 구한 뒤, CRT 이용
- $d_{1} = d \pmod{p-1} \Rightarrow M_{1} = C^{d} \pmod{p} = C^{d_{1}} \pmod{p}$
- $d_{2} = d \pmod{p-1} \Rightarrow M_{2} = C^{d} \pmod{p} = C^{d_{2}} \pmod{p}$
- CRT를 사용해 $M_{1} \& M_{2}$로부터 $M$ 계산 $\rightarrow M=M_{2}p(p^{-1} \pmod{q})+M_{1}q(q^{-1} \pmod{p})$
- 장점: 직접 계산 대비 약 4배 빠름
- $C^{d} \pmod{n}은 약 (1.5 \log{d}$ 번의 곱셈 필요
- 곱셈: $O(\log^{2}{n})$, 지수승 계산: $O(\log^3{n})$
- 모듈러 크기를 절반으로 줄여 두 번 반복하는 구조
- $d_{1}, d_{2}, p, q, p^{-1}, q^{-1}$ 저장
📘 중국인 나머지 정리 (CRT)
정의
서로소인 두 수 $n_1, n_2$에 대해, \(\begin{cases} x \equiv a_1 \pmod{n_1} \\ x \equiv a_2 \pmod{n_2} \end{cases}\) 를 만족하는 해 $x$는 $n_1 n_2$ 범위에서 유일하게 존재한다.- 성질
- $n_1, n_2$가 서로소이면 위의 합동식은 항상 해를 가진다.
- 해는 \(x \equiv a_1 n_2 (n_2^{-1} \pmod{n_1}) + a_2 n_1 (n_1^{-1} \pmod{n_2}) \pmod{n_1 n_2}\) 로 구할 수 있다.
- 예시
다음 합동식을 풀어보자: \(\begin{cases} x \equiv 2 \pmod{3} \\ x \equiv 3 \pmod{5} \end{cases}\)$n_1=3, n_2=5$ 일 때,
$\rightarrow 5^{-1} \equiv 2 \pmod{3}, \;\; 3^{-1} \equiv 2 \pmod{5}$
\(\therefore x \equiv 2 \times 5 \times 2 + 3 \times 3 \times 2 = 38 \equiv 8 \pmod{15}\)최종 답: $x \equiv 8 \pmod{15}$
publications
A standardized glucose-insulin-potassium infusion protocol in surgical patients: Use of real clinical data from a clinical data warehouse
Published in Diabetes Research and Clinical Practice, 2021
We proposed and validated a standardized infusion protocol using real-world clinical data from a hospital data warehouse. This work highlights how large-scale clinical datasets can support practical decision-making in surgery.
Recommended citation: Tae-jung Oh, Ji-hyung Kook, Se Young Jung, Duck-Woo Kim, Sung Hee Choi, Hong Bin Kim, Hak Chul Jang (2021). "A standardized glucose-insulin-potassium infusion protocol in surgical patients: Use of real clinical data from a clinical data warehouse." Diabetes Research and Clinical Practice, 174:108756.
Download Paper | Download Bibtex
talks
Paper Deep Dive – HETAL
Published:
Summary:
In this lab meeting, I reviewed HETAL: Efficient Privacy-preserving Transfer Learning with Homomorphic Encryption. Transfer learning is widely used for data-scarce problems by fine-tuning pre-trained models. While previous studies focused mainly on encrypted inference, HETAL is the first practical scheme that enables encrypted training under homomorphic encryption.
🔑 Research Question:
- How can transfer learning be made both privacy-preserving and efficient when client data must remain encrypted?
⚙️ Key Mechanism:
- Encrypted Softmax Approximation: Designed a highly precise softmax approximation algorithm compatible with HE constraints.
- Efficient Matrix Multiplication: Introduced an encrypted matrix multiplication algorithm, 1.8×–323× faster than prior methods.
- End-to-end Encrypted Training: Adopted validation-based early stopping, achieving accuracy comparable to plaintext training.
📊 Main Results:
- Fine-tuning on encrypted models succeeded (a new milestone compared to prior work).
- Training times ranged 567–3442 seconds (< 1 hour) across five benchmark datasets.
- Accuracy comparable to non-encrypted training was achieved.
⚠️ Limitations:
- Accuracy degradation in certain tasks due to approximation constraints.
- Evaluation limited to moderate-sized models/datasets.
Slides:
PDF (Korean) Download
Paper Deep Dive – MaskCRYPT
Published:
Summary:
In this lab meeting, I reviewed MaskCRYPT: Federated Learning With Selective Homomorphic Encryption for Federated Learning. While federated learning protects data from direct leakage, exposing model weights can still lead to serious privacy risks such as membership inference attacks. MASKCRYPT addresses this challenge by selectively encrypting only a small fraction of model updates, striking a balance between security and efficiency under homomorphic encryption.
🔑 Research Question:
- Do we have to encrypt all the model weights?
⚙️ Key Mechanism: Selective Homomorphic Encryption
- Gradient-guided priority list to identify which weights to encrypt.
- Clients generate individual masks, which are then aggregated on the server to form a final Mask Consensus shared with all clients.
- Encrypt only selected weights, while the rest are transmitted as plaintext averages.
📊 Main Results:
- Encrypting as little as 1% of weights effectively defends against membership inference and reconstruction attacks.
- Reduced communication overhead by up to 4.15× compared with encrypting all model updates.
- Improved wall-clock training time.
- Maintained accuracy comparable to non-encrypted training.
⚠️ Limitations:
- Clients must exchange local priority lists, introducing overhead.
- Correctness and fairness of the Mask Consensus mechanism must be guaranteed.
- Evaluated only on moderate-sized models/datasets.
Slides:
PDF (Korean) Download
Federated Unlearning: Concept & Challenges
Published:
Summary:
In preparation for a lab meeting, I studied the concept of Federated Unlearning, which extends the idea of “machine unlearning” to federated learning environments. While federated learning protects raw data by keeping it on clients, requests such as the “Right to be Forgotten” raise a crucial question: How can we safely remove the influence of specific data or clients from a trained federated model? This summary is based on the PEPR ’24 talk Learning and Unlearning Your Data in Federated Settings (USENIX).
🔑 Research Question:
- Can federated learning systems support safe and efficient data deletion without full retraining?
⚙️ Conceptual Approaches:
- Passive Unlearning:
- Server-only (leveraging stored updates)
- Client-aided (clients assist with gradient/history)
- Active Unlearning:
- Server and clients collaboratively remove the influence of target data.
- Level of Unlearning:
- Record-level, class-level, or client-level unlearning
📊 Key Insightes:
- Retraining is reliable but computationally prohibitive.
- Approximate unlearning can preserve accuracy but may weaken guarantees.
- Privacy, consistency, and efficiency must be carefully balanced.
- Lack of formal proof of unlearning remains a major challenge.
⚠️ Limitations & Open Challenges:
- Verifiability: proving that unlearning actually occurred.
- Dynamic participation: handling clients joining or leaving.
- Fairness and explainability remain underexplored.
- New privacy risks may arise during the unlearning process itself.
🎥 Reference:
- PEPR ‘24 - Learning and Unlearning Your Data in Federated Settings
Slides:
PDF (Korean) Download
Paper Deep Dive – FedRecovery
Published:
Summary:
For the lab meeting, I prepared a review of FedRecovery: Differentially Private Machine Unlearning for Federated Learning Frameworks. Machine unlearning aims to make models “forget” specific client data upon deletion requests. Unlike retraining-based solutions, which are often infeasible or risky in federated learning, FedRecovery introduces an efficient method to erase a client’s influence from the global model using a weighted sum of gradient residuals and differential privacy noise, without assuming convexity.
🔑 Research Question:
- Can we efficiently find a model that performs similarly to the retrained one?
⚙️ Key Mechanism:
- Removes client contributions via weighted gradient residual subtraction.
- Adds carefully tailored Gaussian noise to guarantee indistinguishability between unlearned and retrained models.
- Does not require retraining-based calibration or convexity assumptions.
📊 Main Results:
- Achieves statistical indistinguishability between unlearned and retrained models.
- Experimental results on real-world datasets show comparable accuracy to retrained models.
- Significantly more efficient than retraining-based approaches.
⚠️ Limitations / Open Questions:
- Trade-offs in noise calibration vs. model utility.
- Applicability to very large-scale, complex neural networks not fully explored.
❓ Data Privacy Problem
- Paper Assumption: Unlearning requires the server to identify which client’s updates to remove. Local DP allows this with noisy updates, but homomorphic encryption makes it infeasible, since encrypted updates are indistinguishable, deletion requests lose meaning.
- Naive Idea: Instead of abandoning encryption, the deletion-requesting client could send its past updates multiplied by -1, encrypted under homomorphic encryption. This would effectively cancel its previous contribution without revealing raw gradients, offering a potential direction for client-assisted unlearning under encryption.
Slides:
PDF (Korean) Download